07 Time & Work
| Site: | KINGS EDUCATION - Best MCA coaching, NIMCET coaching in Jaipur |
| Course: | Digital Books |
| Book: | 07 Time & Work |
| Printed by: | Guest user |
| Date: | Tuesday, 25 November 2025, 10:44 AM |
1. Introduction
Time and work is one of the important topics from which directly or indirectly many questions are asked in CAT and other management entrance examinations. This chapter is based on the concept of direct and inverse variations. We need to understand relation among time, work done and number of employees working.
Assuming that all employees work with the same efficiency, we can conclude that work done is directly proportional to number of employees working and number of days to complete the work is inversely proportional to number of employees working. For example if a person does a work in \(x\) days then in 1 day he does only \(\frac{1}{x}\)th of the work and in \(n\) number of days, he will complete \(\frac{n}{x}\) part of the work. Similarly if two men can complete a work working alone in 10 and 20 days respectively, then one day’s work of both the men will be \(\frac{1}{{10}} + \frac{1}{{20}} = \frac{3}{{20}}\). Thus the total work can be completed by both of them in \(\frac{1}{{3/20}} = \frac{{20}}{3}\) days.
2. Various Parameters in Time and Work
In this chapter, there are many parameters like number of men, working hours, efficiency, amount of work etc.
Assuming that all employees work with same efficiency, we can conclude that if the work done is constant then the number of days is inversely proportional to the number of employees working.
\(M \propto \frac{1}{D}\), where \(M\) is the number of employees.
\( \Rightarrow MD\) = constant
Thus we obtain a relationship
\({M_1}{D_1} = {M_2}{D_2}\)
If work is not constant, then it is directly proportional to both number of employees and number of days
\(\frac{{{M_1}{D_1}}}{{{W_1}}} = \frac{{{M_2}{D_2}}}{{{W_2}}}\) = constant
Important points:
- If \(A\) can do a piece of work in \(X\) days, then A’s one day’s work = \(\frac{1}{X}th\) part of whole work.
- If A’s one days’ work = \(\frac{1}{X}th\) part of whole work, then \(A\) can finish the work in \(X\) days.
- If A can do a piece of work in \(X\) days and \(B\) can do it in \(Y\) days then \(A\) and \(B\) working together will do the same work in\(\frac{{XY}}{{X + Y}}\) days.
- If \(A, B\) and \(C\) can do a work in \(X,Y\) and \(Z\) days respectively then all of them working together can finish the work in \(\frac{{XYZ}}{{XY + YZ + XZ}}\) days.
Example 1: \(A\) can do a piece of work in 20 days and \(B\) can do it in 12 days. How long will they take, if both work together?
Solution: There are different methods to solve this problem.
(i) Unitary Method: A can do \(\frac{1}{{20}}th\) of the work in one day, and B can do \(\frac{1}{{12}}th\) of the work in one day. Hence one day‘s work of \(A\) and \(B\) together will be \(\frac{1}{{20}} + \frac{1}{{12}} = \frac{{3
+ 5}}{{60}} = \frac{8}{{60}}\)
Hence total number of days required =\(\frac{{60}}{8} = 7\frac{1}{2}\,\,days\)
(ii) LCM Method: \(A\) can do the work in 20 days while \(B\) can do the same work in 12 days.
Let the total work be \(LCM (20, 12) = 60\) units
Contribution of \(A\) per day = \(\frac{{60}}{{20}} = 3\) unit
Contribution of \(B\) per day = \(\frac{{60}}{{12}} = 5\) unit
Thus, contribution of both is 3 + 5 = 8 units in a day. Thus, total days required is = \(\frac{{60}}{8} = 7\frac{1}{2}\;days\)
Example 2: If \(X\) can do a work in 10 day, \(Y\) can do the same work in 20 days, \(Z\) can do double of the work in 30 days. If all 3 started working together, find the total time required to complete the work.
Solution:
(i) Unitary Method: One day’s work of \(X\) = \(\frac{1}{{10}}\)
One day’s work of \(Y\) and \(Z\) will be \(\frac{1}{{20}}\) and \(\frac{1}{{15}}\)
Because \(Z\) completes double of the work in 30 days,
Combined work done in one day
\(\frac{1}{{10}} + \frac{1}{{20}} + \frac{1}{{15}} = \frac{{6 + 3 + 4}}{{60}} = \frac{{13}}{{60}}\)
Hence total time taken = \(\frac{{60}}{{13}}\,\, = \,\,4\frac{8}{{13}} = 4.61\) days
(ii) LCM Method: \(X\) can do the work in 10 days while \(Y\) can do the same work in 20 days and \(Z\) can do it in 15 days.
Let the total work be \(LCM (10, 20, 15) = 60\) units
Contribution of \(X\) per day = \(\frac{{60}}{{10}} = 6\) units
Contribution of \(Y\) per day = \(\frac{{60}}{{20}} = 3\) units
Contribution of \(Z\) per day = \(\frac{{60}}{{15}} = 4\) units
Thus, contribution of all of them is \(6 + 3 + 4 = 13\) units in a day.
Thus, total days required is = \(\frac{{60}}{{13}} = 4\frac{8}{{13}}\;days\)
Example 3: Working alone, Anil can do a job in 12 days and Vinay can do the same job in 15 days. Anil starts working and works for 6 days and then Vinay joins him. In how many days will the job be completed?
Solution: Working alone, Anil can do the job in 12 days, Therefore, in 6 days he will complete half the job.
Vinay and Anil together can complete \(\frac{1}{{12}} + \frac{1}{{15}}\)
\( = \frac{{5 + 4}}{{60}} = \frac{3}{{20}}th\)of the job a day. Therefore, it will take \(\frac{{20}}{3}\) days to complete the whole work and they will take only \(\frac{{10}}{3}\) days to complete half of the work. Hence, the total time taken
= 6 + \(\frac{{10}}{3}days\,\, = \,\,\frac{{28}}{3}days\) \( = \,9\,\frac{1}{3}days\)
Alternate method: Let total work be 60 units (LCM of 12 days and 15 days). That means, Anil can do 5 units/day and Vinay can do 4 units/day. Anil worked 6 days alone so he does 30 units in these days remaining 30 units will be done by Anil and Vinay together. Together they can do
5 + 4 = 9 units/day so they will finish the remaining work in \(\frac{{30}}{9}\) days. Hence, the total time taken = \(6 +\frac{{10}}{3}days\,\, = \,\,\frac{{28}}{3}days\)\( = \,9\,\frac{1}{3}days\).
3. Some Solved Examples
Example 4: Rahul takes 25 days to finish a job alone, while Avinash takes 10 days to finish the same job. What is the ratio of their efficiency?
Solution: Rahul needs 25 days and Avinash needs 10 days to do the work then ratio of time taken by Rahul and Avinash is 5 : 2. The efficiency will be in the ratio 2 : 5 as efficiency is inversely proportional to the time taken. Thus Avinash is 2.5 times faster than Rahul.
Example 5: If Damru is thrice as efficient as Kamru and is therefore able to finish piece of work in 48 days less than Kamru, find the time in which Damru and Kamru can complete can complete the work working together?
Solution: Suppose Damru takes x days to complete the work, then Kamru will take 3x days to complete the same work. Given that
\(3x-x = {\rm{ }}48 \Rightarrow x = {\rm{ }}24\) and \(3x = 72\).
Thus, Damru needs 24 days while Kamru needs 72 days to complete the work independently.
Thus one day’s work of Damru and kamru will be: \(\frac{1}{{24}} + \frac{1}{{72}} = \frac{1}{{18}}\). Thus total time required to complete the work together will be 18 days.
Example 6: It takes 6 technicians a total of 10 hours to build a new server from direct Computer, with each working at the same rate. If six technicians start to build the server at 11:00 AM, and one technician per hour is added beginning at 5:00 PM, at what time will the server be complete?
Solution: Total time taken to build the server = 60 man hours. 6 of them start at 11:00 AM and work till 5 PM. They will complete \(6 \times 6{\rm{ }} = {\rm{ }}36\) man hours of work. At 5 PM they will have 24 more man hours of work to complete.
Between 5 PM and 6 PM they will complete 7 man hours.
Between 6 PM and 7 PM they will complete 8 man hours.
Between 7 PM and 8 PM they will complete 9 man hours.
So, totally they will complete 36 + 7 + 8 + 9 = 60 man hours by 8PM.
Example 7: \(A, B\) and \(C\) can complete a work working alone in 10, 20 and 60 days respectively. \(A\) started the work and after 2 days and \(B\) & \(C\) also joined him. Find the total time required to complete the work.
Solution: The following diagram indicates the workings of \(A, B\) and \(C\).
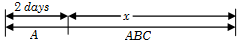
Work done by \(A\) in the first 2 days \( = \,\,\,\frac{2}{{10}} = \frac{1}{5}\)
Remaining work (i.e. 4/5) is completed by \(A, B\) and \(C\) together.
Hence \(x = \frac{{4/5}}{{\frac{1}{{10}} + \frac{1}{{20}} + \frac{1}{{20}}}} = \frac{{48}}{{6 + 3 + 1}} = 4.8\,\,\,days\)
Hence total time occupied = \(2 + 4.8 = 6.8\) days
Example 8: \(A\) and \(B\) working together can complete a work in \(\frac{{20}}{3}\)days, while \(B\) and \(C\) can complete in \(\frac{{60}}{7}\) days and \(A\) and \(C\) can do the work in \(\frac{{15}}{2}\) days. What is number of days required for \(A, B\) and \(C\) to complete the work independently.
Solution: Work done by \(A\) and \(B\) in 1 day = \(\frac{3}{{20}}\)
Work done by \(B\) and \(C\) in 1 day = \(\frac{7}{{60}}\)
Work done by \(C\) and \(A\) in 1 day = \(\frac{2}{{15}}\)
Thus, work done by \(A, B\) and \(C\) together in 1 day
\(\frac{1}{2}\left( {\frac{3}{{20}} + \frac{7}{{60}} + \frac{2}{{15}}} \right) = \frac{1}{2}\left( {\frac{{9 + 7 + 8}}{{60}}} \right) = \frac{1}{5}\)
Thus, work done by \(C\) in one day = \(\frac{1}{5} - \frac{3}{{20}} = \frac{1}{{20}}\)
\(B\) in one day = \(\frac{1}{5} - \frac{2}{{15}} = \frac{1}{{15}}\)
\(A\) in one day = \(\frac{1}{5} - \frac{7}{{60}} = \frac{1}{{12}}\)
Thus, the number of days required by \(A, B\) and \(C\) independently are 12, 15 and 20 respectively.
2. By taking LCM
Let the work be LCM of \(\frac{{20}}{3},\frac{{60}}{7},\frac{{15}}{2} = \frac{{60}}{1}\)units
Contribution of \(A\) and \(B\) = \(\frac{{60}}{{20/3}} = 60 \times \frac{3}{{20}} = 9\)
Contribution of \(B\) and \(C = \frac{{60}}{{60/7}} = 60 \times \frac{7}{{60}} = 7\)
Contribution of \(A\) and \(C = \frac{{60}}{{15/2}} = 60 \times \frac{2}{{15}} = 8\)
Contribution of \(A, B\) and \(C = \frac{{9 + 7 + 8}}{2} = 12\)
Contribution of \(A\) in one day
= Contribution by \((A + B + C)\) - contribution by
\((B + C) = 12 - 7 = 5\)
Thus, number of days required days by A to complete the work is
= \(\frac{{Number\,of\,units}}{{Contribution\;of\;\,A}} = \frac{{60}}{5} = 12\)
Similarly, we can find the required number of days for \(B\) and \(C\).
Example 9: \(A\) is twice as efficient as \(B\) and they complete a work in 12 days. Find the times required by each to complete the work individually.
Solution: When we say A is twice as efficient as \(B\). it means that \(A\) will take half the time taken by \(B\) to complete the work individually suppose \(B\) takes \(2x\) days to complete the work alone then \(A\) will take \(x\) days to complete the same work alone.
Hence \(\frac{1}{x} + \frac{1}{{2x}} = \frac{1}{{12}}\)
\(\therefore \frac{3}{{2x}} = \frac{1}{{12}} \Rightarrow x = \frac{{12 \times 3}}{2} = 18\)
Hence \(A\) and \(B\) will take 18 and 36 days respectively to complete the work working alone
Example 10: \(A, B, C\) can complete a certain project working alone in 10, 15 and 20 days respectively. They worked on this project together for 2 days, then \(A\) left. \(B\) left the project one day earlier than the completion of the project. Find the total time to complete the project.
Solution: The following diagram shows the working of \(A, B\) and \(C\).
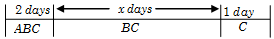
We see that \(C\) has worked for \((x + 3)\) days, \(A\) has worked for 2 days and \(B\) has worked for \((x + 2)\) days.
Hence \((x + 3)\left[ {\frac{1}{{20}}} \right] + (2 + x)\left[ {\frac{1}{{15}}} \right] + \frac{2}{{10}} = 1\)
or \(7x = {\rm{ }}31 \Rightarrow \) \(x =\frac{{31}}{7}\)
Total time taken =\(2 + 1 + \frac{{31}}{7}\) =\(\frac{{52}}{7}\) days
Example 11: 30 men can do a work in 10 days working together. All men started the work together but after 3 days, 10 men left. Find total time required to complete the work
Solution: Total work = \(30 \times 10{\rm{ }} = {\rm{ }}300\) man days.
Total work done in first 3 days
\( = {\rm{ }}3 \times 30{\rm{ }} = {\rm{ }}90\) man days
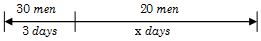
Remaining work = 300 - 90 = 210
Time required \( = \frac{{210}}{{20}} = 10.5\) days
Hence total time required = 3 + 10.5 = 13.5 days
4. Alternate Working
In the following example, we will discuss how to find the total time taken to complete the work, if the two or more workers are not working together but they are working on alternate days. Suppose \(A\) and \(B\) are the two workers working on a project such that \(A\) and \(B\) can complete a work working alone in 20 and 12 days respectively. Now they are working on alternate day, now to find the total time required to complete the work, there can be two cases:
(a) Starting with \(‘A’\)
(b) Starting with \(‘B’\)
In these types of questions work done on the first day is not same as the work done on the second day but work done in first two days is same as the work done in the next two days and that is same as the work done in the nest two days and so on.
AB AB AB ………
Work done in 2 days = \(\frac{1}{{20}} + \frac{1}{{12}} = \frac{{3 + 5}}{{60}} = \frac{8}{{60}} = \frac{2}{{15}}\)
If we assume 2 days to be one cycle and total work is always considered as 1 unit, then approximate number of cycles required to complete the work
= \(\frac{{15}}{2} = 7\) (integral number)
Total work done after 7 complete cycles = \(7 \times \frac{2}{{15}}\)
= \(\frac{{14}}{{15}}\). Hence the remaining work is \(\frac{1}{{15}}\)
(1) A started the work: In one day \(A\) completes \(\frac{1}{{20}}th\) of the work, hence \(\frac{1}{{15}}th\) of the work will be completed in more than one day. \(A\) will complete \(\frac{1}{{20}}th\) part and the remaining work will be done by \(B\).
Remaining work =\(\frac{1}{{15}} - \frac{1}{{20}} = \frac{{4 - 3}}{{60}} = \frac{1}{{60}}\)
Now \(B\) will complete the remaining work in \(\frac{1}{{60}} \times 12 = \frac{1}{5}\) days. Total time taken will be: \({\rm{14 }} + {\rm{ 1 }} + \frac{1}{5} = 15\frac{1}{5}\)
(2) \(B\) started the work: \(B\) will complete the remaining work \(\left( {\frac{1}{{15}}th} \right)\) of the complete work in \(\frac{1}{{15}} \times 12 = \frac{4}{5}\) days
Example 12: \(A, B, C\) can complete a work working alone in 20, 12 and 30 days. If they work on alternate days starting with \(‘A’\) find total time required to complete the work.
Solution: In this question work done on the first day is not same as work done on the second day but work done in the first 3 days = work done in the next 3 days
ABC ABC ………………..
Suppose 3 days mean one cycle, hence work done in one cycle
=\(\frac{1}{{20}} + \frac{1}{{12}} + \frac{1}{{30}}\, = \frac{{3 + 5 + 2}}{{60}} = \frac{{10}}{{60}} = \frac{1}{6}\)
Hence total cycles required = 6
Total cycles required = \(6 \times 3{\rm{ }} = {\rm{ }}18\) days
5. Concept of Man-Days
Man days are an equivalent unit of work. For example, if we say that 20 men can do a work in 30 days, this means that total work is \(20 \times 30\) man days = 600 man days, which means that the same work can be done by 10 men in 60 days or 60 men can do in 10 days only etc. So for a constant work number of man days is constant. Following examples are based on this concept.
Example 13: 10 men or 20 women or 30 children can do a work in 15 days. If 10 men, 12 women and 18 children work on the same work, find the time in which work can be completed.
Solution: We see that 10 men are equivalent to 20 women that is equivalent to 30 children
Hence 1 man \( \equiv \)2 women \( \equiv \)3 children
Total work is \(10 \times15\) = 150 man days
10 men, 12 women and 18 children are equivalent to 10 + (12/2) + (18/3) = 22 men.
Hence time taken to complete the work
= 150/22 = 75/11 = \(6\frac{9}{{11}}\) days.
Example 14: 30 man can do a work in 10 days working together. If this work is started by 1 man next day one more man joins and so on. Find on which day work is complete.
Solution: Total work = \(30 \times 10{\rm{ }} = {\rm{ }}300\) man days
Work done on the first day = 1 man day
Work done on the second day = 2 man days
Work done on the third day = 3 man days and so on.
After \(n\) days, the total work done = \(\frac{{n(n + 1)}}{2}\)
\( = {\rm{ }}300 \Rightarrow n\left( {n + {\rm{ }}1} \right){\rm{ }} = {\rm{ }}600\) or \(n = 24\).
Hence on 24th day work will be completed
Example 15: 4 men and 6 women finish a work in 8 days, while 3 men and 7 women finish it in 10 days. In how many days will 10 women finish it?
Solution: Suppose one day’s work of a man and a woman are \(x\) and \(y\) respectively. From the given information,
\(4x + 6y = \frac{1}{8}\) and \(3x + 7y = \frac{1}{{10}}\)
Solving these equations we get, \(x = \frac{{11}}{{400}}\) and
\(y =\frac{1}{{400}}\)
Work done by the 10 women in one day
= \(\frac{{10}}{{400}}\)=\(\frac{1}{{40}}\)
Hence total time required = 40days.
Example 16: If 5 men and 10 women can do a work in 6 days, same work can be done by 2 men and 9 women in 10 days. In how many days work will be completed by 3 men and 4 women.
Solution: \(5m + 10w\) can do a work in 6 days thus \(6(5m + 10w)\) can do the work in 1 day.
\(2m + 9w\) can do the work in 10 days
Thus, \(10(2m + 9w)\) can do the same work in 1 day
So, \(6(5m + 10w) = 10(2m + 9w)\)
\(30m + {\rm{ }}60w = {\rm{ }}20m + {\rm{ }}90w \Rightarrow \;m = {\rm{ }}3w\)
Thus, efficiency of 1 man is thrice of the efficiency of a woman.
Now, \(5m + {\rm{ }}10w = {\rm{ }}5{\rm{ }} \times {\rm{ }}3w + {\rm{ }}10w\) and efficiency of 3 men + 4 women is equal to \(3 \times 3\) women + 4 women = 13 woman \((1m = 3w)\)
when, \({m_1} = {\rm{ }}25,{d_1} = {\rm{ }}6,{m_2} = {\rm{ }}13,{d_2} = {\rm{ }}?\)
\(25{\rm{ }} \times {\rm{ }}6{\rm{ }} \times {\rm{ }}1{\rm{ }} = {\rm{ }}13{\rm{ }} \times {d_2} \times {\rm{ }}1\) (men days concept)
\({d_2}\) = \(\frac{{150}}{{13}}\) i.e. 11\(\frac{7}{{13}}\) days
6. Pipes and Cisterns
This is the topic which gives the relation between the time required to fill or empty the tank with the taps opened or closed.
Till the time we have only defined the concept of positive work but in the problems related to pipes and cisterns we have to define the concept of negative work also. Concept of negative work is defined as when the work is done against the requirement.
Example 20: Pipe \(A\) fills a tank in 24 minutes. Pipe \(B\) fills the same tank 7 times faster than pipe \(A\). If both the pipes are kept open when the tank is empty, how long will it take for the tank to overflow?
Solution: Pipe \(B\) will fill the tank in \(\frac{{24}}{7}\) minutes as it is 7 times faster than pipe \(A\).
Together, the two pipes will fill \(\frac{1}{{24}} + \frac{7}{{24}} = \frac{8}{{24}} = \frac{1}{3}rd\) of the tank in a minute. So, it will take 3 minutes for the tank to overflow.
Example 21: A tap can fill a tank in 16 minutes and another can empty it in 8 minutes. If the tank is already 1/2 full and both the taps are opened together, will the tank be filled or emptied? How long will it take before the tank is either filled or emptied completely?
Solution: If both the pumps are opened together, then the tank will be emptied because the working efficiency of pump empting is more than that of the pump filling it. Thus in 1 min net proportion of the volume of tank filled
= \(\frac{1}{{16}} - \frac{1}{8} = - \frac{1}{{16}}\)
(Which means that tank will be emptied 1/16th in one minute.) Hence in 8 minutes half of the tank will be emptied.
Example 22: A pump can be operated both for filling a tank and for emptying it. The capacity of tank is \(2400{\rm{ }}{m^3}\). The emptying capacity of the pump is \(10{\rm{ }}{m^3}\) per minute higher than its filling capacity. Consequently, the pump needs 8 minutes less to empty the tank to fill it. Find the filling-capacity of pump.
Solution: Let the filling capacity of the pump is \(x{\rm{ }} {m^3}/min\), then the emptying capacity of the pump will be \(\left( {x + {\rm{ }}10} \right){m^3}\)/min.
Hence \(\frac{{2400}}{x} = \frac{{2400}}{{x + 10}} + 8\)
Solving this we get \(x = {\rm{ }}50{\rm{ }}{m^3}\)/min
Example 23: \(A\) and \(B\) are two pipes which can fill a tank in 8 and 12 hr respectively. \(C\) alone can empty the same tank in 24 hrs. if all three pipes are opened for alternate hours starting with \(A\), in how much time an empty tank can be filled?
Solution: In one cycle fraction of tank filled
\(\frac{1}{8} + \frac{1}{{12}} - \frac{1}{{24}} = \frac{4}{{24}} = \frac{1}{6}\)
But we can’t conclude that it will take 6 complete cycle to fill the tank completely. Because at the last hour only pipe \(C\) is working and that is an emptying pipe hence, after 5 cycle, 5/6th of the tank is full. Next hour \(A\) alone can fill 1/8th part and remaining \((1/6 - 1/8) = 1/24th\) part, \(B\) alone can fill in \(\frac{1}{2}\) hr
Total time required = \(5 \times 3{\rm{ }} + {\rm{ }}1{\rm{ }} + {\rm{ }}1/2\) = \(16\frac{1}{2}\)hr
Example 24: In how many minutes can a tank be filled by three pipes whose diameters are 20 cm, 30 cm and 60 cm? Given that the largest pipe alone can fill it in 49 min.
Solution: We know that rate of flow is directly proportional to the cross section area of the pipe and cross sectional area of the pipe is directly proportional to the square of the diameter.
Ratio of filling rates = \(4 : 9 : 36\)
Total time taken \( = \frac{{36 \times 49}}{{4 + 9 + 36}} = 36\) min
Example 25: Two pipes \(A\) and \(B\) can fill a cistern in 15 hours and 30 hours respectively. There is also an outlet \(c\). If all the three pipes are opened together the tank is full in 45 hours. How much time will be taken by \(C\) to empty the full tank?
Solution: Suppose \(C\) can empty the tank in \(x\) hours working alone
\( \Rightarrow \)\(\frac{1}{{45}} = \frac{1}{{15}} + \frac{1}{{30}} - \frac{1}{x}\)
\( \Rightarrow \) = \(\frac{1}{x} = \left( {\frac{1}{{15}} + \frac{1}{{30}} - \frac{1}{{45}}} \right)\) = \(\frac{{6 + 3 - 2}}{{90}} = \frac{7}{{90}}\)
\(\therefore \) C can empty the full tank in \(\frac{{90}}{7}\) hours.