08 Time, Speed and Distance
| Site: | KINGS EDUCATION - Best MCA coaching, NIMCET coaching in Jaipur |
| Course: | Digital Books |
| Book: | 08 Time, Speed and Distance |
| Printed by: | Guest user |
| Date: | Wednesday, 14 January 2026, 7:16 PM |
1. Introduction
Time speed and distance is very important topic for various entrance examinations. The entire topic revolves around only one concept i.e. \[\rm{Speed} =\frac{{{\rm{Distance}}}}{{{\rm{Time}}}}\]
In this topic we will limit our discussion only to those cases where speed is constant.
UNITS USED
The following conversions will be useful
1 hour = 60 minutes = 3600 seconds
1 km = 1000 m
Approximately 1 mile = \(\frac{8}{5}\) km
1 yard = 3 feet and 1 foot = 12 inches
The commonly used units of speed are km/hr or m/s. The conversion factors of these units are given below:
Speeds in m/s =\(\frac{5}{{18}} \times\) speed in km/hr
Speed in km/hr =\(\frac{{18}}{5} \times\) speed in m/s
For example, a speed of 72 km/hr is equivalent to \(\frac{5}{{18}} \times 72\) = 20 m/s
Or speed of 40 m/s = \(\frac{{18}}{5} \times 40\) = 144 km/hr
Example 1:A car is moving with a speed of 72 km/hr, in how many minutes it can cover a distance of 600 m.
Thus the time taken by the car to cover the distance = \(\frac{{600}}{{20}}\) = 30 sec = 0.5 minutes.
2. Inverse and Direct Relations of Speed, Time and Distance
(a) When distance is constant, time is inversely proportional to speed, which means if speed is doubled, time taken will be halved, if speed becomes one third, time taken becomes tripled etc. the following example explains the concept in details.
Example 2:If a student increases his speed by \(33\frac{1}{3}\% \), he reaches his school 20 min early. Find the usual time taken by the student to reach the school.
When a man drives his car 25% faster than his usual speed he reaches his office 30 minutes earlier than the usual time. At what percent of the usual speed should he drive so that he reaches his office 20 minutes late than the usual time?
The speed of the man is 25% more than the usual = \((5/4)s\)
Hence time taken will be 4/5 of the normal time i.e. \((4/5)T\)
So time saved = \(T/5 = 30\) or \(T = 150\) m.
Now the man wants to reach 20 min late. Hence speed should be \(\frac{{150}}{{170}} = \frac{{15}}{{17}}\) times (= 88.24%) of usual speed.
(b) When the time is constant, then the distance covered is directly proportional to the time taken. This concept is generally used in cases when two or more objects start moving together and they meet after a certain time.
Example 4:\(A, B\) start moving from a point P towards \(Q\). Ratio of the speed of \(A\) & \(B\) is 7:3 \(A\) after reaching \(Q\), returns towards \(P\). Find the point where they meet. Given that \(PQ = 200\) m.
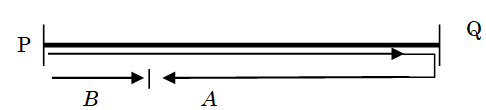
By the diagram, we see that total distance covered by \(A\) & \(B\) together is 400 m. Ratio of distances covered by \(A\) & \(B\) is 7:3
B covered \(3 \times \) \(\frac{1}{{10}}\) \( \times 400\) = 120
So they meet at a point i.e. 120 m away from \(P\).
Example 5: A man coves a certain distance on scooter. Had he moved 3 km/hr faster, he would have taken 20 min less. If he had moved 2 km/hr slower, he would have taken 20 min more. Find the original speed.
Solution: Suppose the original speed is \(v\) and the original time taken is \(t\) min, then \[\frac{{(v + 3)(t - 20)}}{{60}} = \frac{{vt}}{{60}} = \frac{{(v - 2)(t + 20)}}{{60}}\]
From the above relations,
\( \Rightarrow 3t-{\rm{ }}20v = {\rm{ }}60\) and
\(- 2t + 20v = 40\)
Solving these equations we have,
\(t = 100\) min and \(v = 12\) km/hr
Also the distance = \(12 \times \frac{{100}}{{60}} = 20km\)
Note: A man covers a certain distance \(D\). If he moves \(‘u’\) kmph faster, he would have taken \(T\) time less and if he moves \(‘v’\) kmph slower, he would have taken \(T\) time more. The original speed is given by \(\cfrac{{2uv}}{{u - v}}\)
Example 6: A boy walking at a speed of 10 km/h reaches his school 12 min late. Next time at a speed of 15 km/h reaches his school 7 min late. Find the distance of his school from his house?
Solution: Increase in the speed is 50%, it means that the speed becomes \(\frac{3}{2}\) times, thus the time taken must be \(\frac{2}{3}\) times of the initial time and one third of the time is saved. Initial time is 12 min late and now the time taken is 7 min late. Difference between the time = \(12 - 7 = 5\) min
Thus one third of the time is 5 min, or the initial time must be 15 min and the initial speed us 10 km/hr. Thus total distance = \(10 \times \frac{{15}}{{60}} = 2.5\) km.
Example 7: A train after moving 70 kms meets with an accident and it speed becomes 3/4th of the original hence it reaches the destination 36 minutes late. Had the accident been at 85 kms from the starting point the train would have been late only by 24 minutes late. Find the speed of the train.
Solution: Suppose usual speed of the train is v and the distance \(PQ = x\)
Method I:
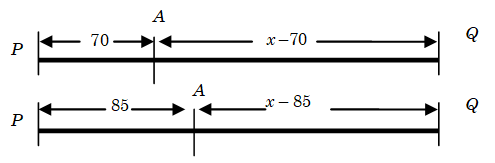
According to the first condition:
\(\frac{{70}}{v} + \frac{{x - 70}}{{\frac{3}{4}v}} = \frac{x}{v} + \frac{{36}}{{60}}\) (1)
\(\frac{{85}}{v} + \frac{{x - 85}}{{\frac{3}{4}v}} = \frac{x}{v} + \frac{{24}}{{60}}\) (2)
Subtracting equation (2) from (1), we get
\(-\frac{{15}}{v} + \frac{{15}}{{\frac{3}{4}v}} = \frac{{12}}{{60}}\) \( \Rightarrow \) v = 25 kms/hour.
Method II: we observe that the difference in the time is because of the middle 15 kms. In the first case train is running at normal speed and in the second case it is running at 3/4th of the normal speed.
\(\frac{{15}}{{(\frac{3}{4}v)}} - \frac{{15}}{v} = \frac{{12}}{{60}}\)
Hence \(v = 25\) km/hr
Example 8: If A travels at 50 kmph he reaches his college 14 minutes late and if he increases his speed to 60 kmph he reaches 16 minutes too soon. Find the distance he is traveling.
Solution: \(\frac{x}{{50}} - \frac{x}{{60}} = \frac{{16 + 14}}{{60}}\)
\(\frac{x}{{300}} = \frac{1}{2}\)\( \Rightarrow x\) = 150 km.
3. Relative Speed
When two bodies are moving in same direction with speeds \({S_1}\) and \({S_2}\) respectively, their relative sped is the difference of their speeds.
Relative Speed = \({S_1} - {S_2}\).
When two bodies are moving in opposite direction with speeds \({S_1}\) and \({S_2}\) respectively, their relative speed is the sum of their speeds.
Relative Speed = \({S_1} + {S_2}\)
Example 9: Two persons A and B started from the same place and in the same direction, after 2 hours distance between them is observed is 3.6 km, if the speed of the faster man is 2 m/s, find the speed of the other man.
Solution: Suppose the speed of the other man is \(x\), then their relative speed is \(2 - x\) and the distance between them after 2 hours is 3.6 km, thus
\(2{\rm{ }} \times {\rm{ }}60{\rm{ }} \times {\rm{ }}60{\rm{ }} \times {\rm{ }}\left( {2{\rm{ }}--x} \right){\rm{ }} = {\rm{ }}3600 \Rightarrow 2{\rm{ }}--x = {\rm{ }}0.5\)
or \(x = 1.5\) m/s
CROSSING OF TWO TRAINS
If 2 trains are running in the same directions, their speeds are \({V_1}\) & \({V_2}\) and their length are \({L_1}\) & \({L_2}\)
Time taken by faster train to over take the slower train
T = \(\frac{{{L_1} + L2}}{{{V_1} - {V_2}}}\)
In opposite direction time taken to cross each other = \(\frac{{{L_1} + {L_2}}}{{V1 + V2}}\)
Time taken by a train of length \(L1\), to cross the platform of length \(L\)
\(=\frac{{L + {L_1}}}{V}\), where \(V\) is the speed of the train.
Example 10: A train 110 m in length travels at 60 km/h. How much time does the train take in passing a man walking at 6 km/hr against the train?
Solution: Relative speeds of the train and the man = (60 + 6) = 66 km/h = \(\frac{{66 \times 5}}{{18}}m/s\)
Distance = 110 m
Therefore, time taken in passing the men
= \(\frac{{110 \times 8}}{{66 \times 5}} = 6\) sec.
Example 11: A cyclist is moving at the speed of 18 Km/hr. Because of the fog he can see only up to 100 m, if a train whose length is 200 mts. overtaking the cyclist and visible to cyclist only for 15 sec. Find speed of train ?
Solution: Total distance traveled by the train w.r.t. the cyclist is 300 mts., hence
\(\frac{{300}}{{v - 5}}\) = 15 sec or \(v = 25\) m/sec = 90 km/hr
Example 12: Two trains 137 meters and 163 meters in lengths are running towards each other on parallel lines, one at the rate of 42 kmps and another at 48 kmph. In what time will they be clear of each other from the moment the meet?
Solution: Relative speed of the trains = \((42 + 48)\)
\(= 90 kmph = 90 \times \frac{5}{{18}}= 25\) m/sec.
Time taken by the trains to pass each other
\( = \left( {\frac{{137 + 163}}{{25}}} \right) = \frac{{300}}{{25}}\)= 12 sec.
4. Special Case
Suppose the two persons \(A\) and \(B\) start moving simultaneously from the points \(P\) and \(Q\) respectively. They meet at a point \(R\) after a time \(T\) and take \({t_A}\) and \({t_B}\) time to reach the point \(Q\) and \(P\) respectively.

Let the distances \(PR\) and \(RQ\) are \(x\) and \(y\) and speeds of \(A\) and \(B\) are \({V_A}\) and \({V_B},\) then
\(x = {V_a} \times T\) (1)
\(y = {V_b} \times T\) (2)
\(x = {t_B} \times {V_B}\) (3)
\(y = {t_A} \times {V_A}\) (4)
Now from the above equations,
\(\therefore \) \(\frac{{{V_A}}}{{{V_B}}} = \sqrt {\frac{{{t_B}}}{{{t_A}}}} \) and \(T = \sqrt {{t_A}{t_B}} \)
In the above case, \(A\) and \(B\) start at the same time and after meeting they take unequal times to reach their destination. Note that if two persons start at the different times but after meeting at a point, they take equal times to reach their destinations, then same formula can be applied.
Example 13: A train starts from \(A\) to \(B\) and another form \(B\) to \(A\) at the same time. After crossing each other they complete their journey in \(3\frac{1}{2}\) and \(2\frac{4}{7}\) hours respectively. If the speed of the first train is 60 km/h, then find the speed of the second train.
Solution: Suppose speed of the second train is \(u\), then \(\frac{u}{{60}} = \sqrt {\frac{{3\frac{1}{2}}}{{2\frac{4}{7}}}} = \sqrt {\frac{{49}}{{36}}} = \frac{7}{6}\)
\( \Rightarrow u = {\rm{ }}70\) km/hr
5. Average Speed
Average speed is always defined as total distance covered in unit time. It is not always equal to average of the speeds.
Average speed = \(\left[ {\frac{{{\rm{total distance}}}}{{{\rm{total time}}}}} \right]\)
For example if a man goes to office @ 20 km/hr and comes back @ 30 km/hr then the average speed will not be equal to \(\frac{{{\rm{20}} + {\rm{30}}}}{{\rm{2}}}\)= 25
Average speed = \(\frac{{x + x}}{{\frac{{\rm{x}}}{{{\rm{20}}}} + \frac{x}{{30}}}}\) = \(\frac{{{\rm{2}} \times {\rm{20 }} \times {\rm{30}}}}{{{\rm{20}} + {\rm{30}}}}\)= 24 km/hr.
In general if an object first covers a distance at a speed of u and then covers the same distance at the speed of v, then its average speed = \(\frac{{2uv}}{{v + u}}\)
Example 14: If a person goes around an equilateral triangle shaped field at speed of 10, 20 and 40 km/h on the first, second and third side respectively and reaches back to the starting point, then find his average speed during the journey.
Solution: Let the measure of each side of triangle is \(D\) km. The person traveled the distance from \(A\) to \(B\) with 10 kmph, \(B\) to \(C\) with 20 kmph and \(C\) to \(A\) with 40 kmph.
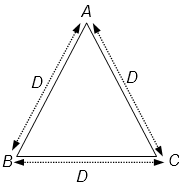
If \({T_{AB}} = \) Time taken by the person to travel from \(A\) to \(B\), \({T_{BC}} = \) Time taken by the persons to travel from \(B\) to \(C\) and \({T_{CA}} = \) Time taken by the persons to travel from \(C\) to \(A\).
Then total time = \({T_{AB}} + {\rm{ }}{T_{BC}} + {\rm{ }}{T_{CA}}\)
\( = \frac{D}{{10}} + \frac{D}{{20}} + \frac{D}{{40}} = D\left( {\frac{{8 + 4 + 2}}{{80}}} \right) = \frac{{7D}}{{40}}\)
Total distance traveled = \(D + D + D = 3D\)
Hence, Average speed
= \(\frac{{3D}}{{7D/40}} = \frac{{120}}{7} = 17\frac{1}{7}kmph.\)
Note that it can be easily proven that if a person moves on the sides of an equilateral triangle with the speeds \({u_1},\,{u_2}\,\& \,{u_3}\) and returns to the initial place, then his average speed will be
\(\frac{{3{u_1}{u_2}{u_3}}}{{{u_1}{u_2} + {u_2}{u_3} + {u_3}{u_1}}}\)
6. Boats and Streams
When a boat is moving in the same direction as the stream or water current, it is said to be moving WITH THE STREAM OR CURRENT.
When a boat is moving in a direction opposite to that of the stream or water current, it is said to be moving AGAINST THE STREAM OR CURRENT.
If the boat is moving with a certain speed in water that is not moving, the speed of the boat is then called SPEED OF THE BOAT IN STILL WATER.
When the boat is moving upstream, the speed of the water opposes (and hence reduces) the speed of the boat.
When the boat is moving downstream the speed of the water adds to the speed of the boat. Thus, we have
Speed of the boat against stream = Speed of the boat in still water - Speed of the stream
Speed of the boat with stream = Speed of the boat in still water + Speed of the stream
These two speeds, the speed of the boat against the stream and the speed of the boat with the stream, are RELATIVE SPEEDS.
If \(U\) is the speed of the boat down the stream and \(V\) is the speed of the boat up the stream, then we have the following relationship.
Speed of the boat in still water = \[\frac{{U + V}}{2}\]
Speed of the water current = \[\frac{{U - V}}{2}\]
In problems, instead of a boat, it may be a swimmer but the approach is exactly the same. Instead of boats / swimmers in water, it could also be a cyclist cycling against or along the wind. The approach to solving the problems still remains the same.
Example 15: A boat travels 30 km upstream in 5 hours and 100 km downstream in 10 hours. Find the speed of the boat in still water and the speed of the stream.
Solution:
Upstream speed = \(\frac{{{\rm{30}}}}{{\rm{5}}}\)= 6 kmph, Downstream speed is \(\frac{{{\rm{100}}}}{{{\rm{10}}}}\) = 10 kmph.
Speed in still water = \(\frac{{{\rm{6}} + {\rm{10}}}}{{\rm{2}}}\) = 8 kmph
Speed of the stream = \(\frac{{10 - 6}}{2}\) = 2 kmph
Example 16: A cycle track is a right triangle with a difference of 2 km between the legs. Its hypotenuse passes along a side road and the two legs pass along a highway. One of the participants of the cycle race took the side road and raced with the speed of 30 km/h and then he covered the two intervals along the highway during the same time with the speed of 42 km/h. Find the length of the race track.
Solution: Cyclist covered hypotenuse with a speed of 30 km/h and the remaining two sides with the speed of 42 km/h taking same time. Hence ratio of the lengths of hypotenuse and the remaining two sides is 30 : 42 = 10:14.
Since difference in the sides is 2, and their sum is 14, hence sides are 8 and 6, length of the track is 24 km.
7. Races and Circular Tracks
When two persons \(P\) and \(Q\) are running a race, they can start the race at the same time or one of them, may start a little later than the other. In the second case, suppose \(P\) starts the race and after 5 seconds, \(Q\) starts. Then we say \(P\) has a “start” of 5 seconds. Alternatively, in a race between \(P\) and \(Q\), \(P\) starts first and then when \(P\) has covered a distance of 10 meters, \(Q\) starts. Then we say that \(P\) has a “start” of 10 meters.
In a race between \(P\) and \(Q\) where \(Q\) is the winner, by the time \(Q\) reaches the winning post, if \(P\) still has another 15 meters to reach the winning post, then we say that \(Q\) has won the race by 15 meters. Similarly, if \(P\) reaches the winning post 10 seconds after \(Q\) reaches it, then we say that \(Q\) has won the race by 10 seconds.
In problems on RACES, we normally consider a 100 m race or a 1 km race. The length of the track NEED NOT necessarily be one of the two figures mentioned above but can be as given in the problem.
When two or more persons running around a circular track (starting at the same point and at the same time), then we will be interested in two main issues:
when they will meet for the first time and
when they will meet for the first time at the starting point
To solve the problems on circular tracks, you should keep the following points in mind.
When two persons are running around a circular track in OPPOSITE directions, the relative speed is equal to the sum of the speeds of the two individuals and from one meeting point to the next meeting point, the two of them TOGETHER cover a distance equal to the length of the track.
When two persons are running around a circular tack in the SAME direction the relative speed is equal to the difference of the speeds of the two individuals and from one meeting point to the next meeting point, the faster person covers one COMPLETE ROUND more than the slower person. We can now tabulate the time taken by the persons to meet for the first time ever or for the first time at the starting point in various cases.
When TWO people are running around a circular track
Let the two people A and B with respective speeds of A and \(B (A > B)\) be running around a circular track (of length L) starting at the same point and at the same time.
Then,

Please note that when we have to find out the time taken by the two persons to meet for the first time at the staring point, what we have to do is to find out the time taken by each of them to complete one full round and then take the LCM of these two timings (L/A and L/B are the timings taken by the two of them respectively to complete on full round.
Example 17: there are three persons \(A, B\) and \(C\). They are running in the same direction, around a circular track of length 120 m. Their speeds are 20, 15 and 10 m/sec. If they start at the same time from the same point, find the time after which they will meet for the first time.
Solution: \({T_{AB}}\) is the time taken when A will over take B for the first time,
then \({T_{AB}}\) = \(\frac{{{\rm{length}}\,\,{\rm{of}}\,\,{\rm{the}}\,\,{\rm{path}}}}{{{\rm{Speed}}\,\,{\rm{of}}\,\,{\rm{A}} - {\rm{speed}}\,\,{\rm{of}}\,\,{\rm{B}}}}\)
\({T_{AB}}\) = \(\frac{{120}}{{20 - 15}} = 24\) sec
Similarly \({T_{AC}}\) is the time when \(A\) will also overtake \(C\), then
\({T_{AC}}\) = \(\frac{{{\rm{length}}\,\,{\rm{of}}\,\,{\rm{the}}\,\,{\rm{path}}}}{{{\rm{Speed}}\,\,{\rm{of}}\,\,{\rm{A}} - {\rm{speed}}\,\,{\rm{of}}\,{\rm{C}}}}\)=\(\frac{{120}}{{20 - 10}} = 12\,\sec \)
Required time is LCM of 24 and 12 sec = 24 sec.
Example 18: There are three persons \(A, B\) and \(C\). They are running around a circular track in the same direction. They can complete one round of this circle in 1 min, 3min and 5 min respectively. If they start at the same time from the same point, find the time after which they will meet for the first time.
Solution: Suppose circumference of the circular path is 15 meter (LCM of 1, 3, 5). So speeds of \(A, B\) and \(C\) will be 15, 5 and 3 m/min.
Suppose \({T_{AB}}\) is the time taken when \(A\) will over take \(B\) for the first time, then
\({T_{AB}}\) = \(\frac{{{\rm{length}}\,\,{\rm{of}}\,\,{\rm{the}}\,\,{\rm{path}}}}{{{\rm{Speed}}\,\,{\rm{of}}\,\,{\rm{A}} - {\rm{speed}}\,\,{\rm{of}}\,\,{\rm{B}}}}\)
\({T_{AB}}\) = \(\frac{{15}}{{15 - 5}} = \frac{3}{2}\)
Similarly \({T_{AC}}\) is the time when \(A\) will also overtake \(C\), then
\({T_{AC}}\) = \(\frac{{{\rm{length}}\,\,{\rm{of}}\,\,{\rm{the}}\,\,{\rm{path}}}}{{{\rm{Speed}}\,\,{\rm{of}}\,\,{\rm{A}} - {\rm{speed}}\,\,{\rm{of}}\,\,{\rm{B}}}}\)=\(\frac{{15}}{{15 - 3}} = \frac{5}{4}\)
Now the required time when \(A, B\) and \(C\) will be at the same place for the first time will be LCM of \({T_{AB}}\) and \({T_{AC}}\)
Hence the required time = LCM of \(\frac{3}{2}\,\,{\rm{and}}\,\,\frac{5}{4}\) = \(\frac{{15}}{2}\)
= 7.5 minutes