What is a cyclic quadrilateral? 

A quadrilateral whose all four vertices lie on a circle is known as a cyclic quadrilateral, or a quadrilateral for which a circle can be circumscribed so that it passes through all four vertices. It is important to note that not all quadrilaterals are cyclic. 

Cyclic Quadrilateral Theorems 

The relations among the four angles of a cyclic quadrilateral, or relations in sides and the diagonals of a cyclic quadrilateral, are known as cyclic quadrilateral theorems. There are some important theorems which prove the properties of cyclic quadrilaterals:

Theorem 1: In a cyclic quadrilateral, the sum of either pair of opposite angles is always 180°. \[\bbox[5px, border:1px solid blue]{\angle A + \angle C = \angle B + \angle D = 180^\circ}\]

Theorem 2: The area of a cyclic quadrilateral is given by \[ \bbox[5px, border:1px solid blue]{\sqrt{(s - a)(s - b)(s - c)(s - d)}} \]where \(s\, = \,\frac{{a + b + c + d}}{2}\) (Semi-perimeter of the quadrilateral)

Theorem 3: If the diagonals are \(p\) and \(q\), then their lengths are given by: \[ \bbox[5px, border:1px solid blue]{p = \sqrt{\frac{(ab + cd)(ac + bd)}{ad + bc}}} \]\[ \bbox[5px, border:1px solid blue]{q = \sqrt{\frac{(ad + bc)(ac + bd)}{ab + cd}}} \]

Theorem 4: In a cyclic quadrilateral, the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides. If \(ABCD\) is a cyclic quadrilateral, then \[\bbox[5px, border:1px solid blue]{AC \times BD = AB \times CD + BC \times DA}\]This property is also known as Ptolemy’s theorem. 

Ptolemy’s Theorem

For a cyclic quadrilateral, the product of the diagonals equals the sum of the products of the opposite sides. 

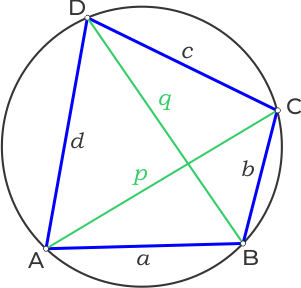
Let the diagonals are \(p\) and \(q\), then \[\bbox[5px, border:1px solid blue]{pq = ac + bd}\]

cyclic Quadrilateral Properties

All the theorems stated above can be summarized as

1. In a cyclic quadrilateral, the sum of either pair of opposite angles is always 180°. Conversely, if the sum of the opposite angles in a quadrilateral is 180°, then the quadrilateral is necessarily cyclic.


2. Area of a cyclic quadrilateral is \(\sqrt {(s - a)(s - b)(s - c)(s - d)} \), where \(s = \frac{{a + b + c + d}}{2}\)


3. For the given four sides a cyclic quadrilateral has the maximum area.


4. If the four sides are \(a,\,\,b,\,\,c,\,\,d\) and the diagonals are \(p\) and \(q\), then \(pq = ac + bd\)


5. A quadrilateral that can be both inscribed and circumscribed on some pair of circles is known as a Bicentric Quadrilateral. If the sides of bicentric Quadrilateral are \(a, b,c,d\), then \(a+c=b+d\). Area of a bicentric quadrilateral having sides \(a,\,b,\,c,\,d\) is \(\sqrt {abcd} \)