Golden ratio is the ratio of the length to the width of the most aesthetically pleasing rectangular shapes. This rectangle, called the Golden Rectangle, appears in nature and is used by humans in both art and architecture. The Golden Ratio can be noticed in the way trees grow, in the proportions of both human and animal bodies, and in the frequency of rabbit births.

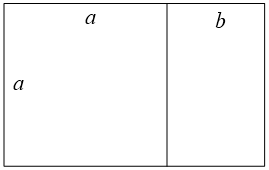
This diagram shows a golden rectangle. The rectangle is divided into a square and a smaller rectangle. In a golden rectangle, the smaller rectangle is the same shape as the larger rectangle, in other words, their sides are proportional. In further words, the two rectangles are similar. This can be used as the definition of a golden rectangle. The proportions give us:

\(\frac{a}{b} = \frac{{a + b}}{a}\)  

This fraction, \(\left( {\frac{{a + b}}{a}} \right)\), is called the golden ratio (or golden section or golden mean).

The ratio is \(\frac{{\sqrt 5  + 1}}{2}:1\) (close to 1.618).

Example 2: If \(\frac{{\sqrt {x + 1}  + \sqrt {x - 1} }}{{\sqrt {x + 1}  - \sqrt {x - 1} }} = \frac{{4x - 1}}{2}\),  find the value of \(x\).

Solution: Applying componendo and dividendo for 2 times, we can easily calculate the value of \(x = {\rm{ }}5/4.\)

Applying first time,

\(\frac{{2\sqrt {x + 1} }}{{2\sqrt {x - 1} }} = \frac{{4x + 1}}{{4x - 3}}\) or

\(\frac{{x + 1}}{{x - 1}} = \frac{{{{(4x + 1)}^2}}}{{{{(4x - 3)}^2}}}\) or x =\(\frac{{{{(4x + 1)}^2} + {{(4x - 3)}^2}}}{{{{(4x + 1)}^2} - {{(4x - 3)}^2}}}\)

x = \(\frac{{32{x^2} - 16x + 10}}{{32x - 8}}\) or \(32{x^2} - 8x = 32{x^2} - 16x + 10\)

\( \Rightarrow \)\(x = \frac{5}{4}\)