Suppose there are two equations, \(x + 2y = 6 \) and \(2x + 4y = 12\), we see that these two equations are not independent. These equations are identical and dependent, so elimination of one variable is not possible. These equations will have infinite numbers of solutions. There are the three different cases, which decide whether there is only one solution, many solutions or no solution: 

• If number of variables is equal to number of independent equations then there is only one solution or no solution.
• If number of independent equations is less than the number of variables, then there are many solutions.
• If the given equations are inconsistent or contradictory, then there is no solution for example. For exmaple, consider the equations \(x + 2y = 5\) and \(2x + 4y = 11\), these equations are contradictory because when \(x + 2y = 5\), then \(2x + 4y\) should be 10 and not 11. These equations do not have any solution and are known as inconsistent equations.

To summarise, suppose the two equations are: 

\({a_1}x + {b_1}x + {c_1} = {\rm{ }}0\) &

\({a_2}x{\rm{ }} + {b_2}x{\rm{ }} + {c_2} = {\rm{ }}0\) 

(1) \(\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}\) , there is only one solution  

(2) \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}\), there are many solutions

(3) \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{{c_2}}}\), there is no solution

Graphical Representation:

Every linear equation represents a straight line when it is drawn on Cartesian system. Geometrically every solution of an equation is a point on the line representing it. Similarly every solution of two equations is the common point of the lines representing the equations. There can be three possible ways in which two lines may intersect. 

1. If two equations are independent and there is only one solution, then these equations represent two straight lines which intersect at only one point and there is a unique solution. 

    

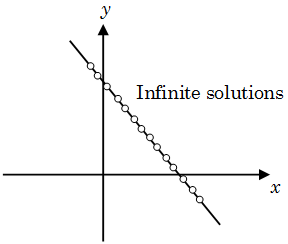
2. If two equations are dependent (that means that there are many solutions), then their graph is pair of lines coincident on each other. 
    
3. If two equations are inconsistent with no solution, then their graph is set of two lines parallel to each other 
   
   

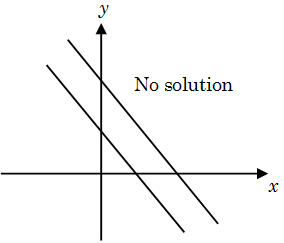
The three graphs shown above represent three cases of the set of linear equations. In the first case the lines are non parallel and intersect at only one point. In the second case both the lines are identical and one lies on the other which means that there are infinite solutions. The third graph shows the case when both the lines are parallel and non-intersecting which indicates that there is no solution.

A linear equation is said to be dependent on other equations if this equation can be formed by using linear combinations of the other equations. For example suppose there are three equations:

\(x + y + z =  3\)       --(1)

\(x - y + 2z = 4\)       --(2)

\(3x + y + 4z = 10\)  --(3) 

Now the third equation is dependent on the first two equations as it can be formed by multiplying equations (1) by 2 and adding it to equation (2).

Example 01: Find the number of solutions of the equations, \(6x + 2y =  13\) & \(9x + 3y  = 19.5\)  

Solution: Comparing the coefficients of the equation

\[\frac{6}{9} = \frac{2}{3} = \frac{{13}}{{19.5}}\]Hence there are many solutions to the set of equations.

Example: Find the number of solutions of the set of  equations \(x + 3y = 4\) and \(x - 3y = 4\)

Solution: Comparing the coefficients of the equation

\(\frac{1}{1} \ne \frac{3}{{ - 3}}\), hence \(\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}\)

There is only one solution to the set of equations.

Example: Find \(k\) if the set of equations has many solutions

\(3x + 4y = 5\)

\(9x + (k + 2) y =15\)

Solution: Two equations have many solutions if 

\(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}{{{c_2}}}\) or \(\frac{3}{9} = \frac{4}{{k + 2}} = \frac{5}{{15}}\)or

\(\frac{4}{{k + 2}} = \frac{1}{3}\) or \(k = 10\)

Example: If \(2x + 3y + 4z = 20\), \(4x + 5y + 8z = 38\) and \(22x + py + 44z = 212\), find the value of \(‘p’\).

Solution:  The value of \(p\) can be found only if the equations are dependent, that means the third equation is a combination of the first two equations. Let equation (3) can be written as  

(\({k_1} \times \)equation (1) \( + {k_2} \times \) equation (2))

Equating coefficients of \(x\) and \(z\),

\( \Rightarrow \)\(2{k_1} + 4{k_2} = 22\) and \(4{k_1} + 8{k_2} = 44\) and 

\(20{k_1} + {\rm{ }}38{k_2} = {\rm{ }}212\)  

\( \Rightarrow \)\({k_1} = 3\,\,and\,\,\,{k_2} = 4\)

Hence  \(p=3\times3 + 4\times5 = 29\)