Suppose there are two types of milk, \(A\) and \(B\), prices of \(A\) and \(B\) are Rs 15 and Rs 20 per litre. If \(A\) and \(B\) are mixed, the mean price of the mixture will be more than 15 and less than 20. Whatever be the ratio of \(A\) and \(B\), mean price can not go beyond the limit 15 and 20. Now, if we mix 3 litres of milk \(A\) and 2 litres of milk \(B\), the mean price will be:

\(\cfrac{{3 \times 15 + 2 \times 20}}{{3 + 2}}\) =\(\frac{{85}}{5}\) = Rs 17 per L

Now instead of this if the mean price is given as 17 Rs/L and we have to find out the ratio of \(A\) and \(B\), Suppose \(A\) and \(B\) are mixed in the ratio of \(x\) and \(y\), then

\(\cfrac{{15x + 20y}}{{x + y}} = 17\) or \(17x +17y =15x + 20y\)
\((17 - 15)x = (20 - 17)y\)  or \(\cfrac{x}{y} = \cfrac{{20 - 17}}{{17 - 15}}\)

Alligation Method:

It can be generalised as \[\color{blue}{\frac{{{\rm{Quantity}}\;{\rm{of}}\;{\rm{cheaper}}}}{{{\rm{Quantity}}\;{\rm{of}}\;{\rm{dearer}}}} = \left[ {\frac{{{\rm{Price}}\;{\rm{of}}\;{\rm{dearer}}\; - \;{\rm{Mean}}\;{\rm{price}}}}{{{\rm{Mean}}\;{\rm{price}} - {\rm{Price}}\;{\rm{of}}\;{\rm{cheaper}}}}} \right]}\]

Using the formula given above, these types of questions can be solved using a diagram given below and the answer can be found instantly.

We can apply the rule in the example solved above, and get the ratio of the quantities of A and B in the mixture

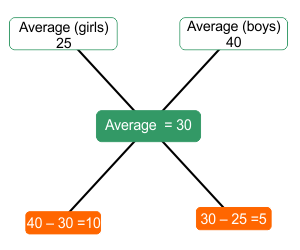
Example 01: What is the ratio of number of girls to the number of boys in a class, if the average weight of the boys is 40 kg and average weight of girls is 25 kg and the average weight of the class is 30.

Solution: Given that the average weight of the boys is 40 kg and average weight of girls is 25 kg.

Example 02: Mohit went to the zoo, where he found some rabbits and sparrows. When he counted number of heads, he found total 110 heads. While when he counted the number of legs he found 360 legs. Find total number of rabbits in the zoo.

Solution: Had there been all rabbits, then there would have been \(110{\rm{ }} \times {\rm{ }}4{\rm{ }} = {\rm{ }}440\) legs

And had there been all sparrows there then there would have been \(110{\rm{ }} \times {\rm{ }}2{\rm{ }} = {\rm{ }}220\) legs

But as there are 360 legs its means neither there are all rabbits nor all are sparrows. There would be some combination of rabbits and sparrows and because of this combination, the number of legs in the combination is 360.

We can solve this question using linear equations also, but to explain the application of Alligation Rule in wide variety of questions, let us solve it using Alligation Rule.

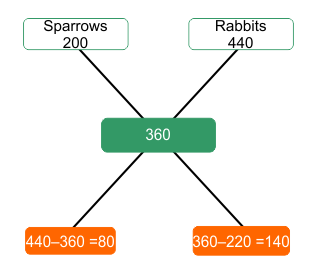
Sparrows and rabbits are in ratio of 80: 140 = 4 : 7

Thus, number of sparrows = \(\frac{4}{{11}} \times 110 = 40\)

Number of rabbits =\(\frac{7}{{11}} \times 110= 70\)

Example 03: Some goods are purchased by Mr. Anil. Some part is sold at a loss of 10% while remaining part is sold at a profit of 35% such that there is a gain of 20% on the whole transaction. Find the ratio of the part sold at loss to the part sold at profit.

Solution: We can consider taking profit on both the goods, note that a loss of 10% means a profit of – 10%. Here one part of the good is sold at – 10% profit and the other part is sold at +35% profit and there is a gain of 20% on the whole transaction, let us use Alligation Rule,

\( \Rightarrow \) Ratio of goods sold at loss to goods sold at profit is 15 : 30 = 1 : 2.