Quadratic Equations
5. Sign of the Quadratic Expression
The quadratic expression \(a{x^2} + bx + c\) can be written as \(a\left\{ {{{\left( {x + \frac{b}{{2a}}} \right)}^2} + \left( {\frac{{4ac - {b^2}}}{{4{a^2}}}} \right)} \right\}\)
We know that \({\left( {x + \frac{b}{{2a}}} \right)^2}\) is always positive, if
\(4ac-{b^2}\) is also positive then sign of the expression is always positive or negative depending on the sign of \(a\).
Case 1: If \(a > 0\), and \(4ac-{b^2}>0\) or \(b^2<4ac\), then sign of the expression is always positive. That means the graph will never cut \(x\) axis and it will always remains above \(x\) axis.
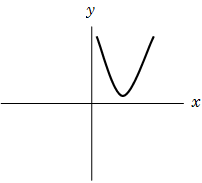
Case 2: If \(a < 0\), and \(4ac-b^2 >0\) or \(b^2 < 4ac\), then sign of the expression is always negative. That means the graph will never cut \(x\) axis and it will always remains below \(x\) axis.
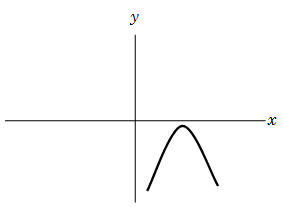
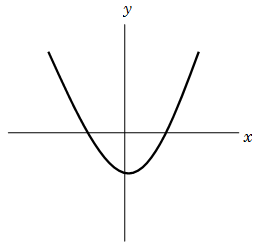
Case 3: If \(4ac-{b^2} < 0\) or \(b^2 > 4ac\), then sign of the expression can be positive or negative both. This graph will intersect \(x\) axis at two distinct points. In other words, the roots of the equation \(ax^2+bx+c=0\)
are real and distinct.
Example 01: If \(3{x^2} - kx + 8\) is always positive for all values of \(x\), find the maximum value of \(k\), where \(k\) is a natural number.
We know that \(a{x^2} + bx + c > 0\) for all values of \(x\), when \(a > 0\) and \({b^2} - 4ac < 0\)
Here \(a > 0\), and \({k^2} - 4 \times 3 \times 8 < 0\)
Hence \( - \sqrt {96} < k < \sqrt {96} \)
Since \(k\) is a natural number hence \(1 \le k \le 9\).
Example 02: If one root of the equation \({x^2} + 2(k - 1)x + k + 5 = 0\) is more than 1 and the other root is less than 1, then find the value of \(k\).
Both the roots are distinct, hence \(4{(k - 1)^2} - 4(k + 5) > 0\)
\( \Rightarrow {k^2} - 3k - 4 > 0\)or \((k + 1)(k - 4) > 0\)
Hence \(k > 4\) or \(k < - 1\)
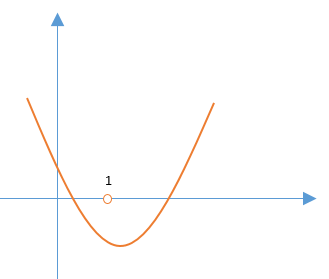

The value of the quadratic expression is negative at \(x = 1\), hence \(3k + 4 < 0 \Rightarrow k < - \frac{4}{3}\)
Combining all the conditions, we have \(k < - \frac{4}{3}\).