Example 01: Solve the equation \({3^{{x^2} - 5x + 8}} + {4^{{x^2} - 5x + 8}} = 25\)

Solution: We know that \({3^2} + {4^2} = {5^2}\), hence \({x^2} - 5x + 8 = 2 \Rightarrow {x^2} - 5x + 6 = 0\) or \(x = 2,\,\,3\).

Example 02: Solve the equation \({(4 + \sqrt 5 )^x} + {(4 - \sqrt 5 )^x} = 8\)

Solution: We see that \((4 + \sqrt 5 ) + (4 - \sqrt 5 ) = 8\), hence \(x = 1\)

Example 03: Solve the equation \({(7 + 4\sqrt 3 )^{{x^2} - 7x + 11}} + {(7 - 4\sqrt 3 )^{{x^2} - 7x + 11}} = 14\)

Solution:  As \((7 + 4\sqrt 3 ) \times (7 - 4\sqrt 3 ) = 1\), hence the numbers \((7 + 4\sqrt 3 ) = \frac{1}{{7 - 4\sqrt 3 }}\)

It is evident from the equation, that \((7 + 4\sqrt 3 ) + (7 - 4\sqrt 3 ) = 14\).

Hence the equation \({(7 + 4\sqrt 3 )^{{x^2} - 7x + 11}} + {(7 - 4\sqrt 3 )^{{x^2} - 7x + 11}} = 14\) is balanced, when are either \({x^2} - 7x + 11 = 1\) or \({x^2} - 7x + 11 =  - 1\)

Solving the two equations, we get values of \(x = 2,\,\,5,\,\,3,\,\,4\)

Example 14: Find all real values of p, for which one root of the equation \({x^2}-{\rm{ }}\left( {p{\rm{ }} + {\rm{ }}1} \right)x{\rm{ }} + {\rm{ }}{p^2} + {\rm{ }}p{\rm{ }}-{\rm{ }}8{\rm{ }} = {\rm{ }}0\) is greater than 2 and other root is smaller than 2.  

Solutions: The graph of this equation is a parabola whose direction is vertically upward as shown in the diagram

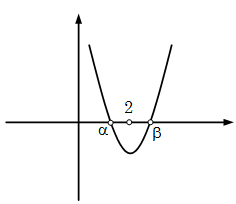
Suppose the roots are \(\alpha \,\,and\,\,\beta \), since one root is more than 2 and one root is less than 2, hence the graph will be negative at \(x = 2\) and  roots are real (as imaginary numbers are not comparable) so \({b^2}-{\rm{ }}4ac > {\rm{ }}0\) and \(f(2) < 0\)

\({b^2}-{\rm{ }}4ac = {\rm{ }}{\left( {p + {\rm{ }}1} \right)^2}-{\rm{ }}4\left( {{p^{2\;}} + p-{\rm{ }}8} \right){\rm{ }} > {\rm{ }}0\)

\(3{p^2} + {\rm{ }}2p-{\rm{ }}33{\rm{ }} < {\rm{ }}0 \Rightarrow \left( {3p + {\rm{ }}11} \right)\left( {p-{\rm{ }}3} \right)\; < {\rm{ }}0\)

\(\therefore \frac{{ - 11}}{3} < p < 3\) ----(1)

Also \(f(2)\) is less than 0, hence 

\(\left( {p-{\rm{ }}3} \right)\left( {p + {\rm{ }}2} \right){\rm{ }} < {\rm{ }}0\) or \(-2 < p < 3\) ----(2)

Combining (1) and (2) we get, \(-2 < p < 3\)