Triangle is shape bounded by three straight lines. A triangle can only be formed by three straight lines, if sum of any two sides is more than the third side and difference of any two sides is less than the third side. These are known as Triangular Inequalities.

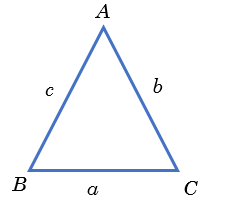
If the sides of the triangle are \(a\), \(b\) and \(c\), then

\[ \bbox[5px, border: 2px solid #0071dc]{ \begin{align*} a+b &> c \\ b+c &> a \\ c+a &> b \end{align*} } \]

Sum of the internal angles:

The sum of the internal angles in a triangle is always 180°. Suppose ABC is a triangle, whose internal angles are \({\theta _1},{\theta _2}\)  and \({\theta _3}.\) Draw a line parallel to BC and passing through A, then 

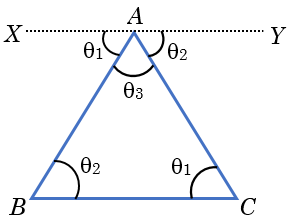
\(\angle \)CAY = \({\theta _1}\) and \(\angle \)XAB = \({\theta _2}\) 

Clearly \(\angle \)XAB + \(\angle \)YAC + \({\theta _3}\) = 180°  

Or \({\theta _1} + {\theta _2} + {\theta _3}\) = 180° 

Internal and external angles in a triangle:

Again extending any of the side, we get external angle. Suppose the line BC is extended to D. Let \(\angle \)ACD = \(\alpha \) 

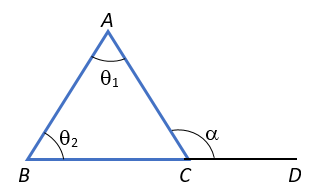
\(\angle \)ACB = 180 – \({\theta _1}\)  – \({\theta _2}\)  = 180 \(-{\alpha}\) 

\(\alpha  = {\theta _1} + {\theta _2}\)

Hence, exterior angle = sum of 2 opposite interior angles.