Geometry
Triangles
Pythagorean Theorem
In a right-angled triangle square of the hypotenuse is equal to the sum of squares of base and height.
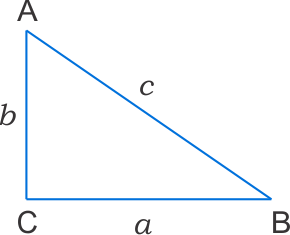
Let ABC be a right angled triangle with side lengths \(a, b\) and \(c\), then \[\bbox[5px, border: 2px solid #0071dc]{{a^2}\; + \;{b^2}\; = \;{c^2}}\]
Pythagorean Triples
A set of three natural numbers \(a, b\) and \(c\) which satisfy the condition \({a^2}\; + \;{b^2}\; = \;{c^2}\) are known as Pythagorean triples. Here is the list of some Pythagorean triples:
(3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25),
(9, 40, 41), (11, 60, 61) etc.
There is a standard method for obtaining all Pythagorean triples. If the Pythagorean Triples are \(a,\,\,b,\,\,c\) then: \[\color{blue}{a = {r^2} - {s^2},{\rm{ }}b = 2rs,\;c = {r^2} + {s^2}}\]
Here \(r > s\) and both \(r\) and \(s\) are not even or odd simultaneously. If one of them is odd, the other is an even number. In the following table, some of the Pythagorean Triples are generated using different values of \(r\) and \(s\).
| \(\color{#0071dc}{s}\) | \(\color{#0071dc}{r}\) | \(\color{#0071dc}{a}\) | \(\color{#0071dc}{b}\) | \(\color{#0071dc}{c}\) |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 15 | 8 | 17 |
| 1 | 6 | 35 | 12 | 37 |
| 1 | 8 | 63 | 16 | 65 |
| 2 | 3 | 5 | 12 | 13 |
| 2 | 5 | 21 | 20 | 29 |
| 2 | 7 | 45 | 28 | 53 |
| 2 | 9 | 77 | 36 | 85 |
| 3 | 4 | 7 | 24 | 25 |
| 3 | 6 | 27 | 36 | 45 |
| 3 | 8 | 55 | 48 | 73 |
| 4 | 5 | 9 | 40 | 41 |
| 4 | 7 | 33 | 56 | 65 |
| 4 | 9 | 65 | 72 | 97 |
A corollary of the Pythagorean Theorem’s converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Where c is chosen to be the longest of the three sides:
- If \({a^2}\; + \;{b^2}\; = \;{c^2}\), then the triangle is right-angled
- If \({c^2} < {a^2}\; + \;{b^2}\), then the triangle is acute angled
- If \({c^2} > {a^2}\; + \;{b^2}\), then the triangle is obtuse-angled