Right Angled Triangle:

In a right angled triangle square of hypotenuse is equal to sum of squares of base and height.

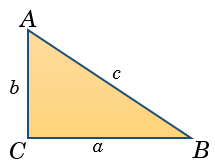
Let ABC be a right angled triangle with side lengths \(a, b\), and \(c\), then \({a^2}\; + \;{b^2}\; = \;{c^2}\).

Acute Angled Triangle

If all the three angles in a triangle are acute, then triangle is known as acute angled triangle.

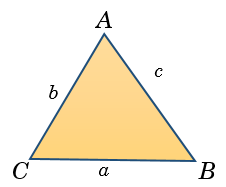
A triangle with sides \(a, b, c\) is an acute angled triangle if 

\({c^2} < {a^2}\; + \;{b^2}\), \({b^2} < {a^2}\; + \;{c^2}\) and  \({a^2} < {b^2}\; + \;{c^2}\)

If \(c\) is the largest side, then only one condition i.e. \({c^2} < {a^2}\; + \;{b^2}\) is sufficient to determine that the triangle is an acute angled triangle.

Obtuse Angled Triangle

If one angle in a triangle is obtuse, then triangle is known as obtuse angled triangle. 

If the sides of a triangle are \(a,\;b,\;c\) and \(c\) is the biggest side, then it will be an obtuse angled triangle if \[{c^2} > {a^2}\; + \;{b^2}\]

Question 01: The sides of a triangle are integers. If the two sides are 8 and 5, find the number of such triangles.

Question 02: Three sides of a triangle are integers and the triangle is an obtuse angled triangle. If the two sides are 8 and 15, find the number of such triangles.