In any triangle \(ABC\), the angle bisector of \(A\) divides the line \(BC\) in the ratio of \(AB\) and \(AC\). This theorem is valid for internal as well as external angle bisector.

If the line \(AD\) is angle bisector (internal as well as external as shown in the diagram)

\[\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}\]

To calculate the length of the angle bisector: 

Suppose in the triangle \(ABC\),\(\angle BAD = \angle DAC = \theta \), now \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}\), suppose \(AB\) and \(AC =  a, b\), then \(BD\) and \(DC\) are in the ratio of \(a\) and \(b\). 

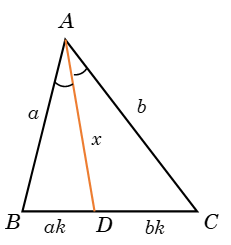
Applying cosine formula in the triangle \(ABD\) and \(ADC\),

\[\cos \theta  = \frac{{{a^2} + {x^2} - {{(ak)}^2}}}{{2ax}} = \frac{{{b^2} + {x^2} - {{(bk)}^2}}}{{2bx}}\]

Solving this we get, \({x^2} = a.b - ab{k^2}\)

\[\Rightarrow{x^2} = ab - (ak)(bk) = AB.AC – BD.DC\]

\[\Rightarrow A{D^2} = AB \times AC - BD \times DC\]

Ceva’s Theorem 

In a triangle \(ABC\), let \(AD, BE\) and \(CF\) meet at a point \(O\), then \[\frac{{AF}}{{FB}}.\frac{{BD}}{{DC}}.\frac{{CE}}{{EA}} = 1\]

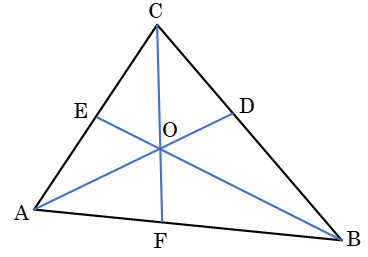
The Converse of the theorem is also true; 

If the points \(D, E\) and \(F\) are taken on \(BC, CA\)  and \(AB\) and \(\frac{{AF}}{{FB}}.\frac{{BD}}{{DC}}.\frac{{CE}}{{EA}} = 1\), then \(AD, BE\) and \(CF\) are concurrent.