Area is generally defined as region bounded or covered by a bounded figure or it is number of unit squares which can be placed inside a bounded figure.

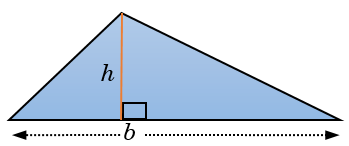
1. \(\color{Blue}{\rm{Area} = \frac{1}{2} \times b \times h}\) 
2. If height is not given but all the sides are given, then area of the triangle can be calculated by Heron’s Formula.
   \(\color{blue}{{\rm{Area}} = \sqrt {s(s - a)(s - b)(s - c)} }\) where \(s\) is semi perimeter and \(s = \frac{{a + b + c}}{2}\) and \(a, b, c\)  are the sides of  triangle.
3. When two sides and angle between them is given, \(\color{blue}{{\rm{Area}} = \frac{1}{2}ab\sin \theta }\)
4. If all side of triangle are equal (Equilateral triangle), \(\color{blue}{{\rm{Area}} =\frac{{\sqrt 3 }}{4}{a^2}}\)
5. \(\color{blue}{{\rm{Area}} = rs}\), where \(r\) is the in-radius and \(s\) is the semi perimeter  (= \(\frac{{a + b + c}}{2}\))
6. \(\color{blue}{{\rm{Area}} = \frac{{abc}}{{4R}}}\), where, \(R\) is the circumradius.

Example: Find area of a triangle whose sides 13, 14 and 15. Also find length of the perpendicular from a vertex to the side of length 15.

Solution: The triangle is shown below:

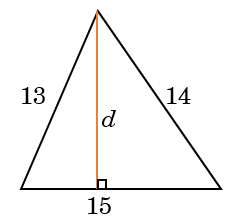
\(s = \frac{{13 + 14 + 15}}{2} = 21\)

So, the area of triangle = \(\sqrt {21 \times (12 - 13) \times (21 - 14) \times (21 - 15)} = 84\) 

Suppose height of the triangle is d, then its area can be written as \(\frac{{15 \times d}}{2} = 84\), or \(d = 11\frac{1}{5}\)

Example: Find length of common chord of two circles whose radii are 13 and 11 and distance between centres is 20 cms. Also find the area of the rectangle that just covers the common part of the two circles.

Solution: By joining centres of the circles we get a triangle whose sides are 13, 11 and 20.

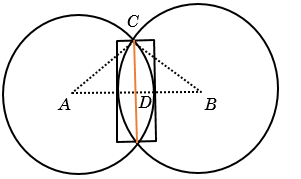
Equate the Area of triangle \(ABC\) using two formulas.

 Area =\(\sqrt {s(s - a)(s - b)(s - c)} \), \(s = \frac{{11 + 13 + 20}}{2} = 22\)  

Area = \(\sqrt {22(22 - 11)(22 - 13)(22 - 20)} \) = 66

Area = \(\frac{{AB \times CD}}{2}\,\, = \,66\) or \(CD = 6.6\)

Length of common chord = 2× 6.6 = 13.2 units.

Width of the rectangle = (13 + 11)  – 20 = 4

Hence area of the rectangle = 4×13.2 = 52.8