Centroid

The centroid is the intersection point of three medians of a triangle. All the three median are concurrent and they divide each other in the ratio 2:1. In the given triangle if \(G\) is the centroid, then \[\frac{{AG}}{{GD}} = \frac{{BG}}{{GE}} = \frac{{CG}}{{GF}} = \frac{2}{1}\]

Incentre:

Incentre is the intersection point of the angle bisectors of three internal angles of a triangle. The incentre is equidistant from three sides of the triangle. The incentre always lies inside the triangle.

In the above triangle, three dotted lines are the angle bisectors and their intersection I is known as incentre. In-centre is equidistant from the three sides. A circle that touches all three circles internally is known as in-circle.

In-radius of a triangle

Let the sides of the triangle be \(a, b\) and \(c\), then in-radius is given by the formula \[\bbox[5px, border: 2px solid #0071dc]{r=\frac{\Delta}{s}}\]Where \(\Delta\) is the area of the triangle and \(s\) is the semi-perimeter of the triangle, \(s=\frac{a+b+c}{2}\).

Circumcentre:

Circumcentre is the intersection point of the three perpendicular bisectors of a triangle. This centre is equidistant from the three vertices. This centre can lie outside the triangle if the triangle is an obtuse angle triangle.

Circum-radius of a triangle

Let the sides of the triangle be \(a, b\) and \(c\), then circum-radius, \(R\), is given by the formula \[\bbox[5px, border: 2px solid #0071dc]{R=\frac{abc}{4\Delta}}\]Where \(\Delta\) is the area of the triangle.

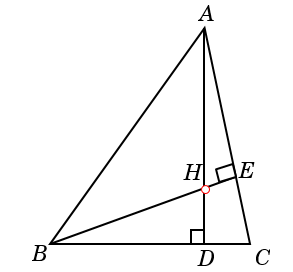
Orthocentre:

Orthocentre is the intersection point of the three altitudes of a triangle. Ortho centre of a triangle can lie inside, outside or at the vertex of a triangle.

In an acute-angled triangle, it lies inside the triangle. In a right-angled triangle, it lies at the vertex, in an obtuse angled triangle it lies outside the triangle. In the given triangle, \(H\) is the orthocentre of the triangle.