ALGEBRAIC FUNCTIONS: An algebraic function is one which consists of a finite number of terms involving powers and roots of the variable \(x\) and the four simple operations: addition, subtraction, multiplication and division. Obviously, all polynomial, rational and irrational functions are algebraic functions.

TRANSCENDENTAL FUNCTIONS: All functions which are not algebraic are called transcendental functions. These functions include:

1. The trigonometric functions as \(\sin x,\,\cos x,\) \(\tan x\) etc.
2. the inverse trigonometric functions as  \(si{n^{-1}}x,{\rm{ }}co{s^{-1}}x,{\rm{ }}ta{n^{-1}}x\) etc ;
3. the exponential functions as \({e^x},{\rm{ }}{10^x}\;\) 
4. logarithmic functions as \(lo{g_a}x,{\rm{ }}log{\rm{ }}\left( {4{\rm{ }}-x} \right)\) etc.

EXPLICT FUNCTIONS:  \(y\) is said to be an explicit function of independent variable \(x\), if we can write \(y = f(x)\), i.e. if \(y\) can be expressed directly in terms of the independent variable \(x\). 

IMPLICIT FUNCTIONS: \(y\) is said to be an implicit function of the independent variable (or variables) \(x\) if it cannot be expressed directly in terms of \(x\). 

For example, \(xy = {x^3} + {y^3}\)

BOUNDED & UNBOUNDED FUNCTIONS: A function \(f(x)\) is said to be bounded above if there exists a fixed number, say \(M\), such that \(f(x)\) is never greater than \(M\) for all values of \(x\) in the given interval and \(M\) is called the upper bound of \(f(x)\) in that interval. The function \(f(x)\) is said to be bounded below if there exists a fixed number, say m, such that \(f(x)\) is never less than \(m\) for all values of \(x\) in the given interval and \(m\) is called the lower bound of \(f(x)\) in that interval. A function \(f(x)\) is said to be bounded on both sides or simply bounded if it is bounded above as well as bounded below, i.e. if there exists two fixed numbers, say \(m\) and \(M\), such that

\(m\) \( \le f(x) \le \) \(M\), for all values of \(x\) in the given interval.

The function \(f(x)\) is said to be unbounded if one or both of the upper and lower bounds of the function are infinite.

PERIODIC FUNCTIONS: A function \(f(x)\) is called a periodic function if there exists a least positive number \(T\) such that \(f(x + T) = f(x)\). \(T\) is called the period of the function \(f(x)\). Obviously, if \(T\) is the period of \(f(x)\), then 

\(f(x) = f(x + T) = f(x + 2T) = f(x + 3T) =... .\)

IDENTITY FUNCTION: A function \(f(x)\) is said to be an identity function if for all real \(x, f(x) = x\). Domain and Range of identity function is all real number.

MODULUS FUNCTION: Modulus function or absolute value function \(f(x)\) is defined as:

\(f(x) = \,\left\{ {\begin{array}{*{20}{c}}x&{if\,x \ge 0}\\{ - x}&{x \le 0}\end{array}} \right.\)

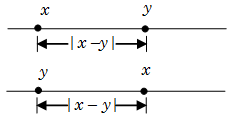
This function is represented as \(\left| x \right|\), and called the modulus function or absolute value function. In other words the absolute value of \(x\) gives the distance between \(x\) and \(0\). It is always positive or zero. For example,

\(\left| 3 \right|{\rm{ }} = {\rm{ }}3,{\rm{ }}\left| {-3} \right|{\rm{ }} = {\rm{ }}3,{\rm{ }}\left| 0 \right| = {\rm{ }}0\).

If \(x\) and \(y\) are two points on a line, then \(\left| {x-y} \right|\) gives distance between \(x\) and \(y\) irrespective of the positions of \(x\) and \(y\).

\(|x - y| = \,\left\{ {\begin{array}{*{20}{c}}{x - y}&{if\,x \ge y}\\{y - x}&{x < y}\end{array}} \right.\) 

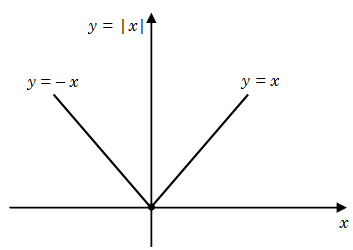
Graph of modulus function: \(f\left( x \right){\rm{ }} = \left| x \right|\)

Example 11: Find the minimum value of the function \(f\left( x \right){\rm{ }} = {\rm{ }}\left| {x{\rm{ }}-{\rm{ }}2} \right|{\rm{ }} + {\rm{ }}\left| {x{\rm{ }}-{\rm{ }}3} \right|{\rm{ }} + {\rm{ }}\left| {x{\rm{ }}-{\rm{ }}7} \right|\), also find the value of \(x\), when \(f(x) = 14\). 

Solution: To determine the minimum value of the function, let us first plot the graph. We know that the graph will be consisting straight lines, and we can easily calculate the value of \(f(x)\) at \(x = 2\), \(3\) and \(7\).

Thus the graph is passing through the points 

(2, 6), (3, 5) and (7, 9).

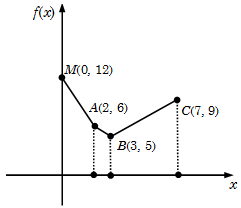
By simple observation we see that the graph is minimum at the point \(x = 3\), and the value of the function at this point is 5.

Now the value of \(f(x)\) is increasing, hence it’s value will be 14, when \(x\) is less than 0 or \(x\) is more than 7.

Case 1: \(x\) is less than \(0\), thus the value of function \(f(x)\) will \((2 - x) + (3 - x) + (7 - x)\)

\(= 12 - 3x\)

Hence \(12 - 3x = 14\) \( \Rightarrow x\) \(=  - \frac{2}{3}\)

Case 2: \(x\) is more than 7, then the function \(f(x)\) will be \((x - 2) + (x - 3) + (x - 7) = 3x - 12\)

Now \(3x - 12 = 14\) \( \Rightarrow x = \frac{{26}}{3}\)

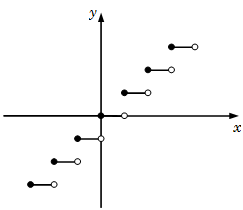
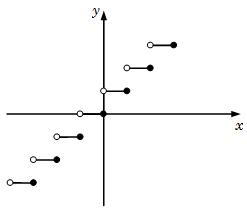
GREATEST INTEGER FUNCTION: Greatest integer functions are also known as Step function or Floor function.

\(f(x) = [x] =\) greatest integer less than or equal to \(x [x] = n\), where \(n\) is an integer such that \(n \le x \le n + 1\) 

For example \([2.9] = 2, [-2.1] = -3\).

The following figure represents the graph of greatest integer function.

Also note that \(f(x) - [f(x)]\) is the fractional part of the function \(f(x)\) and

\(0 \le f(x) - [f(x)] <1\) 

Now consider the case when \(f(x)\) is integer, then \([f(x)] = f(x)\), similarly we can conclude that if \([x] +[y] = x + y\), then \(x\) and \(y\) both are integers.

SMALLEST INTEGER FUNCTION: Least integer function are also known as Ceiling function

For a real number \(x\), we denote by \(\left\lceil x \right\rceil \), the smallest integer greater than or equal to \(x\). For example, \(\left\lceil {5.2} \right\rceil  = 6\), \(\left\lceil { - 5.2} \right\rceil  =  - 5\), etc.

The following figure represents the graph of smallest integer function.

SIGNUM FUNCTION: Signam function is defined as \(\frac{{|x|}}{x}\), when \(x\) is positive signam function has a constant value of 1. When \(x\) is negative, signam function has a value of 1.

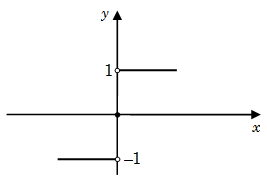
Graph of Signum function

The value of signum function is zero at \(x  = 0\).

ODD and EVEN functions:

If \(f(-x) = f(x)\), then the function \(f(x)\) is even. Even function are symmetrical about \(y\) axis. For example \(cosx,{x^2}\) etc are even functions.

If \(f(-x) = -f(x)\), then the function \(f(x)\) is odd. Odd function are symmetrical in opposite quadrants. For example sin \(x\), \({x^3}\) etc are odd functions.

Some functions may not satisfy any of the above conditions, then these functions are neither even nor odd function

Example 12: Find whether the function 

\(f(x) = \frac{{\cos x\sin x}}{{(\tan x + \cot x)}}\) is even function of \(x\).

Solution:  Here \(f(-x) = \frac{{\cos \left( { - x} \right)\sin \left( { - x} \right)}}{{\tan ( - x) + \cot ( - x)}}\)

=  \(\frac{{ - \cos x\sin x}}{{\tan x - \cot x}}\)=\(\frac{{\cos x\sin x}}{{(\tan x + \cot x)}}\) = f(x).

Hence \(f(x)\) is even functions of \(x\).\(\)