Two triangles are said to be similar if they are in the same shape, now same shape can be decided by different measures

1. The three angles of one triangle are equal to the three angles of the second triangle. The corresponding angles of two similar triangles are equal but the corresponding sides are only proportional and not equal.


2. Two sides of one triangle are proportional to two sides of the other and the included angles are equal, 


3. The three sides of one triangle are proportional to the three sides of another triangle.

In two similar triangles,

1. Side opposite to similar angles bears a constant ratio. Ratio of corresponding sides 
   = ratio of perimeters etc.


2. Since area is proportional to square of the side, hence Ratio of areas = Ratio of squares of corresponding sides for example if ratio of the corresponding sides of two triangles is 1:2, ratio of the corresponding area will be 1:4

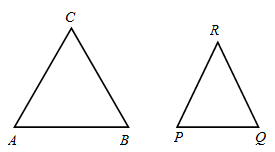
In the above diagram there are two triangles, suppose \(\angle A\) =\(\angle P\) and \(\angle B\) =\(\angle Q\), then triangle become similar. Now,

\(\frac{{BC}}{{AC}} = \frac{{QR}}{{PR}}\) and  \(\frac{{BC}}{{AB}} = \frac{{QR}}{{PQ}}\)

Ratio of the sides opposite to the corresponding same angles will be same.

Remember that in any right angle triangle, if we draw a perpendicular from the right angle, we get two similar triangles as shown in the triangle below.

ABC is a right angled triangle, \(AD \bot \;BC\), then 

Triangle \(ADB \approx \) triangle \(ADC \approx \) triangle \(ABC\)

\(\frac{{AD}}{{BD}}\, = \,\frac{{DC}}{{AD}}\,\, \Rightarrow \,AD{}^2\,\, = \,(BD)(DC)\)

Similarly taking triangles \(ACD\) and \(ABC\), 

\(\frac{{AC}}{{CD}} = \frac{{CB}}{{AC}} \Rightarrow A{C^2} = CD \times CB\)

Similarly \(A{B^2} = BC \times BD\)

Adding \(A{B^2}\) and \(A{C^2}\) we get, \(A{B^2} + A{C^2} = B{C^2}\)

Example: In triangle \(ABC\) if \(\angle A{\rm{ }} = {\rm{ }}90^\circ \). \(PQRS\) is square. If \(RC = 3 BQ = 2\) Find the area of \(PQRS\).

Solution: Suppose side of the square = \(x\) and \(\Delta CSR\) is similar to \(\Delta PQB\)

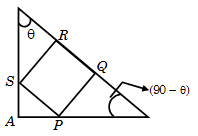
\( \Rightarrow \therefore \frac{x}{2} = \frac{3}{x}\) or  \({x^2} = {\rm{ }}6\)  

Area of the square = \({\left( {side} \right)^2} = {\rm{ }}6\).