In any triangle if we join midpoint of any two sides, then this line will be parallel to the third side and half of the length of the third side.

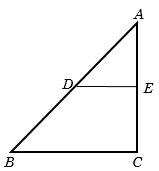
In this triangle \(ADE\) and \(ABC\) are similar triangles. Hence \(DE\) is parallel to \(AB\).

As \(D\) and \(E\) are the mid points, 

\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\)=\(\frac{1}{2}\)

Example 16:  In the triangle \(ABC\), \(DE\) and \(FG\) are parallel to \(AB\) and \(AF: FD: DB = 1:1:1\), find the ratio of the area of \(A1:A2:A3\).

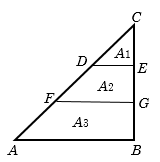
Solution: Triangles \(CDE, CFG\) and \(CAB\) are similar, where, \(CD:CF:CA =1:2:3\)

So, area of these triangles are in the ratio \(1: 4 : 9\) 

\({A_1} = {\rm{ }}1,\;{A_1} + {A_2} = {\rm{ }}4,{A_1} + {A_2} + {\rm{ }}{A_3} + {\rm{ }}9\)

\({A_1} = {\rm{ }}1,{A_2} = {\rm{ }}3,{A_3} = {\rm{ }}5\; \Rightarrow {A_1}:{A_2}:{A_3} = {\rm{ }}1{\rm{ }}:{\rm{ }}3{\rm{ }}:{\rm{ }}5\)