Two triangles are said to be congruent if they are identical in terms of shape and size. In other words, two similar triangles are of the same size, they are said to be congruent. To prove two triangles to be congruent, first we prove that they are similar and then if any of the corresponding side is same, the triangles become identical or congruent. Further two triangles are congruent if : 

1. Three sides of one triangle are respectively equal to the three sides of the second triangle.
2. Two sides and the included angle of one triangle are respectively equal to two sides and the included angle of the second triangle
3. Two angles and one side of a triangle are respectively equal to two angles and the corresponding side of the second triangle

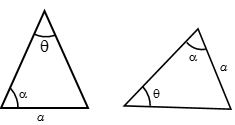
The two triangles shown above are similar as two of the angles are same so third angle is automatically same. Now the side opposite to the angle \(\theta \) is same in both the triangles, thus both  the triangles become congruent as they are not only of same shape but also of same size.

KEY RESULTS

1. Ortho centre is the point where the three altitudes meet each other.
2. Centroid of a triangle is the point where the 3 medians cut each other.
3. In an Isosceles triangle the centroid, the cirumcentre, the orthocentre and the  incentre all lie on the median to the base
4. In an equilateral triangle the centroid, the orthocentre the circum centre and the incentre, all coincide.
5. Inradius is less then half of any of the three altitudes of the triangle.
6. In an acute angled triangle the circum center lies inside thetriangle. In right angled triangle the circum center lies on the hypotenuse of the triangle. In on obtuse angled triangle it lies outside the triangle.
7. In an acute angled triangle orthocenter lies inside the triangle. In right angled triangle it lies on the vertex where the right angle is formed. In obtuse angled triangle, it lies outside the triangle. 
8. In a right angled triangle, the length of the median drawn to the hypotenuse is equal to half the hypotenuse. This median is called the circum radius of the right angled triangle.
9. Circum radius of an equilateral triangle =\(\frac{a}{{\sqrt 3 }}\) and inradius =\(\frac{a}{{2\sqrt 3 }}\)