Any four sided closed figure is called a Quadrilateral. The sum of four angles of a Quadrilateral is equal to \(360^\circ \). The  perpendicular drawn to a diagonal (in a Quadrilateral) from the opposite vertices are called offsets.

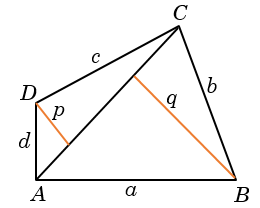
Suppose the length of \(AC\) is \(\ell \), then area of the quadrilateral is  \(\frac{\ell }{2}(p + q)\)

If sum of the opposite angles is \(\alpha \), then area is 

\(\sqrt {(s - a)(s - b)(s - c)(s - d) - (abcd){{\cos }^2}\frac{\alpha }{2}} \)

When sum of the opposite angles is \(180^\circ \), then it is known as a cyclic quadrilateral and its area becomes \[{\rm{Area}} = \sqrt {(s - a)(s - b)(s - c)(s - d)} \]