If one pair of opposite sides of a quadrilateral is parallel, then it is called a trapezium.

The two sides other than the parallel sides in a trapezium are celled as oblique sides. 

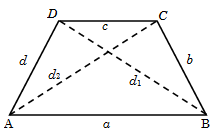
Area of trapezium = \(\frac{1}{2}\left( {a + c} \right) \times h\), where h is the distance between a and  c.

Diagonals are \({d_1}\) and \({d_2}\), 

\({d_1}^2 + {d_2}^2\; = {b^2} + {d^2} + {\rm{ }}2ac\)

If we draw a line parallel to the base and which divides the oblique lines in the ratio \(m : n\) 

In general length of this line 

\(\ell  = \frac{n}{{m + n}}(AB) + \frac{m}{{m + n}}(CD)\)

Further it can be easily concluded that 

\(\frac{n}{m} = \frac{{\ell  - DC}}{{AB - \ell }}\) and heights of the two trapezium are also in the same ratio.

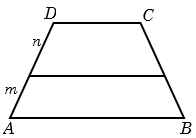
The segment joining the mid-points of the non-parallel sides is called the median of the trapezium. 

Median = \(\frac{1}{2} \times \) sum of the parallel sides

Example 17: \(ABCD\) is a trapezium in which \(AB\) and \(CD\) are parallel. A line \(EF\) of length 15 cm is drawn parallel to the base \(AB\). Find the ratio of areas of \(CDEF\) and \(ABFE\). Given that \(AB = 20\), \(CD = 12\) and height of \(ABCD\) is \(8\).

Solution: Suppose the line \(EF\) divides the line \(AD\) in the ratio \(m : n\), then 

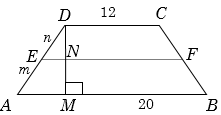
\(EF = \frac{{m \times DC + n \times AB}}{{m + n}}\)

\( \Rightarrow 15 = \frac{{m \times 12 + n \times 20}}{{m + n}}\)

or \(15 m + 15 n = 12 m + 20 n\)

\( \Rightarrow 3m = 5n\) or \(m : n = 5 : 3\) 

Again height of the trapezium \(EFCD\) is \(DN\), then 

\(\frac{{DN}}{n} = \frac{{DM}}{{m + n}}\)  \(\Rightarrow \frac{{DN}}{3} = \frac{8}{{5 + 3}}\) or \(DN = 3\).

Area of trapezium \(EFCD = \left( {\frac{{12 + 15}}{2}} \right) \times 3 = \frac{{81}}{2}\)

Area of trapezium \(ABFE = \left( {\frac{{20 + 15}}{2}} \right) \times 5 = \frac{{175}}{2}\)

Required ratio = \(\frac{{81/2}}{{175/2}} = \frac{{81}}{{175}}\)