A line is called an axis of symmetry of a graph if you can pair the points such that the line is perpendicular of the segment joining the pair of points. Study the graph below to identify the axis of symmetry:

Types of symmetry & Test for symmetry

Symmetry to the \(x\)-axis: In the equation, leave \(x\) alone and replace \(y\) with \(-y\). If you get the same equation, it is symmetric to the \(x\)-axis.

Symmetry to the \(y\)-axis: In the equation, replace \(x\) with \(-x\). If the equation is the same, it is symmetric to the \(y\)-axis.

Symmetry to the line \(y = x\): Interchange \(x\) and \(y\). If the equation is the same then it is symmetric to the line \(y = x\).

Symmetry to the origin: Replace \(x\) with \(-x\) and \(y\) with \(-y\). If the equation is the same, then it is symmetric to the origin.

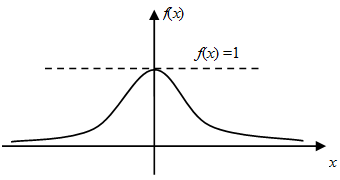
Graph of any function can be plotted by using symmetry, domain and range. Suppose there is a function \(f(x) = {10^{ - {x^2}}}\). Following conclusions can be drawn:

1. The graph will be symmetrical about \(y\) axis. 
2. The value of the graph always positive, as negative powers of \(x\) also give positive values.
3. Graph is defined for all values of \(x\) and it is maximum at \(x = 0\).

So the graph will be like:

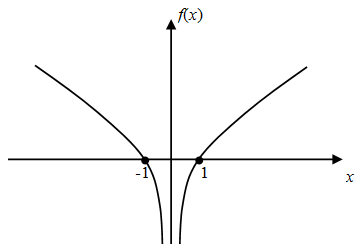
Example: Trace the graph \(f\left( x \right){\rm{ }} = {\rm{ }}lo{g_{10}}\left| x \right|\)

Solution: The graph is symmetrical about \(y\) axis. Lets first draw the graph for positive values of \(x\). The nature of the graph will be increasing. The value of the function will be 0 at \(x =1\) and will be equal to 1 at \(x =10\). at \(x = 0\), value of the function will be \( - \infty \). Now the same graph appears for the negative values of \(x\).

Example 15: Plot the graph \(y = sin x\) and 

\(y = sin 2x\)  and compare them.

Solution: The period of sin x will be \(360°\) and period of \(sin2x\) is \(180°\).

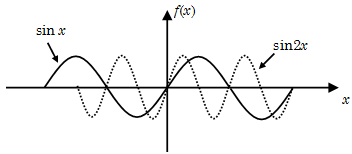
The graph of \(sin2x\) will be shrunk as its period is only \(180°\). But maximum value of \(sin2x\) remains same.

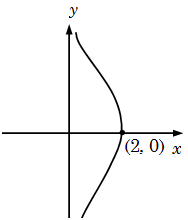
Example 16: Plot the graph \(x{y^2} = {\rm{ }}4\left( {2{\rm{ }}-{\rm{ }}x} \right)\)

Solution: The equation can be written as \({y^2} = \frac{{4(2 - x)}}{x}\)

The graph is symmetrical about x axis. Now \(x\) can not be negative or more than 2 as \({y^2}\) becomes negative and \(y\) becomes imaginary. When \(x\) is tending to 0, \(y\) is tending to infinite. 

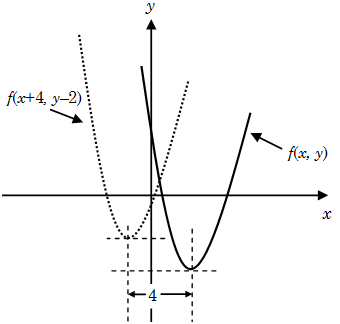
Example 17: If the \(f(x, y)\) is plotted is the following graph. Plot the graph for \(f(x + 4, y - 2)\)

Solution: The function \(f(x, y)\) means \(y = f(x)\) and the function \(f(x + 4, y)\) means \(y = f(x + 4)\). Suppose in the function \(f(x, y)\) at \(x = {\rm{ }}0,y = {y_1}\), now in the second function \(f(x + 4, y)\), at \(x = -4\), the same value of \(y\) can be obtained. If the graph for \(f(x, y)\) is given, then the graph for \(f(x + 4y)\) can be obtained by shifting the graph 4 unit towards left. Similarly graph of \(f(x + 4, y - 2)\) can be obtained by shifting the graph \(f(x + 4, y)\) 2 units vertically upwards.

Example 18: Find the number of solutions of the equation \(\sin x = \frac{x}{{10}}\).

Solution:  We know that \(x\) radian = \(\frac{{180}}{\pi }\) degree.  Hence 10 radian = 570°.

When \(x =10\), \(y\) is 1, hence there is no solution for \(x\) more than 10.

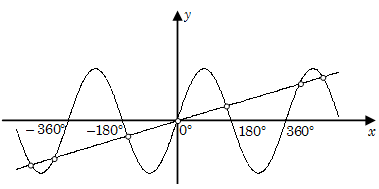
Total number of solution when \(x > 0\), is 3, thus total number of solutions = 7.