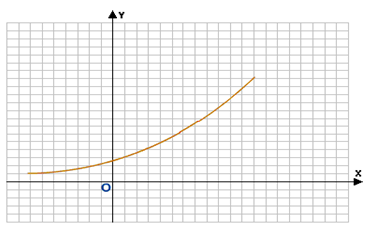
\(y={e^x}\)

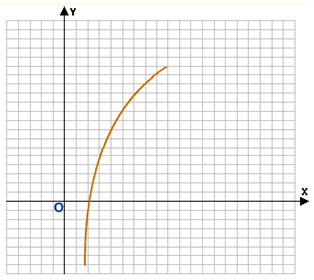
\(y={\log_{10}x}\)

Example 19: If \(g\left( x \right) = \frac{{{9^x}}}{{{9^x} + 3}}\), find the value of 

\(g\left( {\frac{1}{{2009}}} \right) + g\left( {\frac{2}{{2009}}} \right) + ......g\left( {\frac{{2008}}{{2009}}} \right)\)

Solution: \(g\left( {1 - x} \right) = \frac{{{9^{1 - x}}}}{{{9^{1 - x}} + 3}} = \frac{9}{{9 + {{3.9}^x}}} = \frac{3}{{3 + {9^x}}}\)

\(g\left( x \right) + g\left( {1 - x} \right) = \frac{{{9^x}}}{{{9^x} + 3}} + \frac{3}{{3 + {9^x}}} = \frac{{{9^x} + 3}}{{{9^x} + 3}} = 1\)

Hence,  \(f\left( {\frac{1}{{2009}}} \right) + f\left( {\frac{{2008}}{{2009}}} \right) = 1\) &

\(f\left( {\frac{2}{{2009}}} \right) + f\left( {\frac{{2007}}{{2009}}} \right) = 1.....\) and so on.

Required sum = 1004.

Example 20:  What is the area bounded by the graph \(\left| x \right| + \left| y \right| = {\rm{ }}1\)

Solution:  The graph of this equation lies in all four quadrants 

\(\begin{array}{*{20}{c}}{x + y = 1}&{x > 0,y > 0}\\{x - y = 1}&{x > 0,y < 0}\\{ - x + y = 1}&{x < 0,y > 0}\\{ - x - y = 1}&{x < 0,y < 0}\end{array}\)

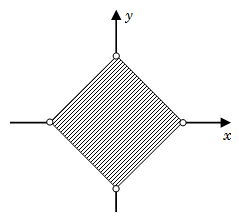
These four lines are making a square. Whose side is\(\sqrt 2 \), hence area of the square is 2.

Example 21: How many times the graphs 

\(f\left( x \right){\rm{ }} = {\rm{ }}1/x{\rm{ }}and{\rm{ }}f\left( x \right){\rm{ }} = {\rm{ }}lo{g_{10}}x\) intersect.

Solution: \(f(x) = 1/x\) is a decreasing graph and 

\(f\left( x \right){\rm{ }} = {\rm{ }}lo{g_{10}}x\) is an increasing function. Hence these graphs intersect at only one point.

Example 22: Find the number of intersection points of the graphs \(y = f(x)\) and \(y = g(x)\), where \(f(x) = 2 + {x^2}\) and \(g(x) = \frac{1}{{\left( {{x^2} + \frac{1}{{{x^2}}}} \right)}}\)

Solution: Since \(f(x)\) is always more than or equal to 2. Also\({x^2} + \frac{1}{{{x^2}}} \ge 2\), thus \(g\left( x \right){\rm{ }} \le {\rm{ }}0.5\), hence the two graphs can never meet.

Example 23: Find \(\phi [\psi \left( x \right)]\) and \(\psi [\phi \left( x \right)]\) if 

\(\phi \left( x \right){\rm{ }} = {\rm{ }}{x^2} + 1\) and \(\psi \left( x \right){\rm{ }} = {\rm{ }}{3^x}\).

Solution: Given that \(\phi \left( x \right){\rm{ }} = {x^2} + 1\) and \(\psi \left( x \right){\rm{ }} = {\rm{ }}{3^x}\)

Hence \(\phi (\psi \left( x \right)){\rm{ }} = \phi \left( {{3^x}} \right){\rm{ }} = {\rm{ }}{\left( {{3^x}} \right)^2} + {\rm{ }}1\) = \({3^{2x}} + 1\)

and \(\psi (\phi \left( x \right)){\rm{ }} = \psi \left( {{x^2} + {\rm{ }}1} \right)\) = \({3^{{x^2} + 1}}.\)

Example 24: Let\(f(x) = \frac{{\alpha x}}{{x + 1}},x \ne  - 1.\)Then, for what value of \(\alpha \) is \(f{f(x)} = x\)?

Solution: \(f\left[ {f(x)} \right] = f\left( {\frac{{\alpha x}}{{x + 1}}} \right) = f(y) = \frac{{\alpha y}}{{y + 1}}\)

Now put \(y = \frac{{\alpha x}}{{x + 1}}\)

\(\therefore f[f(x)] = \frac{{{\alpha ^2}x}}{{(\alpha  + 1)x + 1}} = \frac{x}{1}(as\,\,given)\)

By inspection it is clear that \(\alpha  + {\rm{ }}1{\rm{ }} = {\rm{ }}0\) i.e. \(\alpha  = {\rm{ }}-1\) makes \(f[f(x)] = x\).

Example 25: If \(f(x) = \frac{x}{{\sqrt {1 + {x^2}} }}\) then find the value of \((f\,o\,f\,o\,f)x\)

Solution: \((f\,o\,f)\,x = f[f(x)] = f[t]\)where 

\(t = \frac{x}{{\sqrt {1 + {x^2}} }}\), hence \(f(f(x)) = f(t)\) 

\( \Rightarrow f(f(x) = \frac{t}{{\sqrt {1 + {t^2}} }} = \frac{{x/\sqrt {1 + {x^2}} }}{{\sqrt {1 + {x^2}/(1 + {x^2})} }} = \frac{x}{{\sqrt {1 + 2{x^2}} }}\)

Similarly we calculate the value of \(f(f(f(x))\) as \(\frac{x}{{\sqrt {(1 + 3{x^2})} }}\)

Example 26: If \({T_N} = {\rm{ }}{\left( {{T_{N{\rm{ }}-{\rm{ }}1}}-{\rm{ }}1} \right)^2} + {\rm{ }}1\), where \('N'\) is a natural number \(> 1\), also \({T_1} = {\rm{ }}3\) find \(\frac{{({T_1} \times {T_2} \times {T_3} \times {T_4} \times {T_5} \times ...... \times {T_{10}}) + 1}}{{({T_1} - 1)({T_2} - 1)({T_3} - 1)({T_4} - 1)........({T_{10}} - 1)}}\)

Solution: Given that \({T_N}_{} = {\rm{ }}{\left( {{T_N}_{-{\rm{ }}1}-{\rm{ }}1} \right)^{2\;}} + {\rm{ }}1\)

Let us tabulate the values of \(N\) and \({T_N}\)

Hence, \({T_N}^{} = {2^{{2^{n - 1}}}} + 1\)

Thus the value of the given expression is:

\(\frac{{[({2^1} + 1)({2^2} + 1)({2^4} + 1)....({2^{512}} + 1)] + 1}}{{{2^1} \times {2^2} \times {2^4} \times {{.....2}^{512}}}}\) 

= \(\frac{{{2^{1024}} - 1 + 1}}{{{2^{1023}}}} = 2\)