A Quadrilateral in which opposite side are parallel is called a parallelogram.

1. Opposite sides are equal and parallel, opposite angles are equal.
2. Each diagonal divides the parallelogram in two congruent triangles and diagonals bisect each other.
3. Sum of any two adjacent angles is 180°.
4. Angle bisectors of vertices form a rectangle

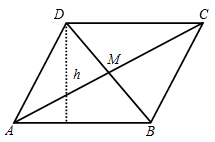
Area of the parallelogram = Base \( \times \) height = \(AB \times h\)

or area = \(AB \times ADsin\theta \), where \(\theta \) is the angle between \(AB\) and \(AD\).

Example 18: In a parallelogram two adjacent sides are 11 and 13 cms, if length of one of the diagonal is 20, find the length of the second diagonal.

Solution: The following diagram shows the parallelogram whose sides are 11 and 13. \(AC\) is  20 or \(AM =10\), suppose \(MD = a\). 

Using Apollonius Theorem

\({11^2} + {\rm{ }}{13^2} = {\rm{ }}2{\rm{ }}\left( {{{10}^2} + {a^2}} \right) \Rightarrow a\) = \(\sqrt {45} \)

\(BD = 2a = 2\sqrt {45} \)