A polygon is traditionally a plane figure that is bounded by a closed path, composed of straight line segments. These segments are called its edges or sides. A convex polygon is one in which each of the interior angles is less than 180°. It can be noticed that any straight line drawn cutting a convex polygon passes only two sides of the polygon, whereas in a concave polygon, it is possible to draw lines passing through more than two sides.

A concave polygon is a non-convex polygon. It can also be defined as a polygon in which at least one angle is more than 180°. 

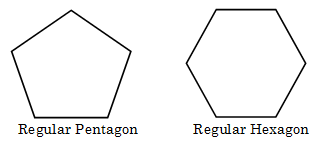
 A regular polygon is a convex polygon in which all sides are equal and all angles are equal. The names of polygons with three, four, five, six, seven, eight, nine, and ten sides are respectively triangle, quadrilateral, pentagon, hexagon, heptagon, octagon, nonagon, and decagon.

The sum of interior angles of a convex or concave polygon is = \(\left( {n-{\rm{ }}2} \right) \times 180\), where \(n\) is the number of the sides of the polygon. 

If each of the sides of a convex polygon is extended, the sum of the external angles thus formed is equal to 4 Right Angles (i.e. 360°). 

For a regular polygon value of each interior angle is \(\frac{{(n - 2) \times 180}}{n}\) and value of exterior angle is \(\frac{{360}}{n}\).

The following table gives name and sum of internal angles of various polygons.