Two polygons are similar if corresponding angles are equal as well as corresponding sides are proportional. For example if there are two rhombuses, and their sides are proportional, there is no surety that these rhombuses are similar until we know that their corresponding angles are same.

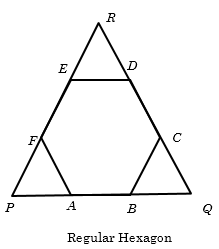
Example 19: A regular hexagon is formed by removing three triangular pieces from an equilateral triangle. If the side of the triangle is 30, find the side of the regular hexagon.

Solution:  If the triangle is \(PQR\) and the regular hexagon is \(ABCDEF\). 

We know that \(\angle FAB = \angle BCD = {120^o}\), hence  \(\angle QBC = \angle QCB = {60^o}\), triangle \(BCQ\) becomes an equilateral triangle. Similarly we can prove that triangle \(EDR\) and \(FPA\) are also equilateral. So \(PA = AB = BQ =\) side of the hexagon. Since side of the triangle \(= 30\), hence side of the hexagon \(= 30/3 =10\)