A sector is a region bounded by two radii and an arc lying between the radii and a segment is a region bounded by a chord and an arc lying between the chord's endpoints. 

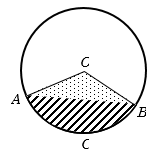
In this diagram the complete region \(OACBO\) is sector and the region \(ACBA\) is segment.

If the angle of the sector is \(\theta\), then 

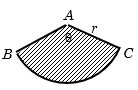
Area of the sector =\(\frac{\theta }{{360}}\pi {r^2}\), Arc length \(BC{\rm{ }} = {\rm{ }}r\theta \)

Area of the segment = area of the sector - area of triangle

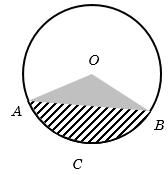
If the angle \(AOB =\theta \) and radius of the circle \(= r\), then 

Area of the segment \(=\frac{\theta }{{360}}\pi {r^2}-\) area of triangle \(OAB\)

\(= \left[ {\frac{\theta }{{360}}\pi {r^2} - \frac{1}{2}{r^2}\sin \theta } \right]\)

Example 20: Find the area of the shaded part where radius of each circle is 10 cms.

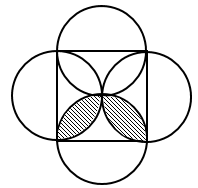
Solution: There are 4 leaves inside the square. Shaded area = area of semicircle – area of two leaves. Let us first draw only one leaf.

Area of one leaf = 2 (area of the shaded part)

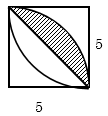
\(= 2\left( {\frac{{\pi ({5^2})}}{4} - \frac{{25}}{2}} \right)\), Hence area of two leaves

\(=4\left( {\frac{{\pi ({5^2})}}{4} - \frac{{25}}{2}} \right)\) =\(25\pi  - 50\)

Example 21: Eight identical circles of largest size are placed in a square of side \(a\), find the radius of each circle.

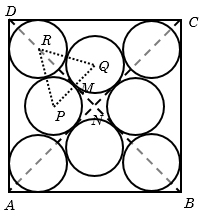
Solution: Suppose radius of each circle is \(r\), then

\(RQ = PQ = PR = 2r\), so the triangle \(PQR\) is an equilateral triangle.

\(RM = \frac{{\sqrt 3 }}{2}(2r)\)=\(\sqrt 3 r\)

\(DR = \sqrt 2 r\), now \(ND = NM + MR+ RD\) 

\(= r +\sqrt 3 r\)+\(\sqrt 2 r\)

Now \(BD = 2(DN) =\sqrt 2 a\), where \(a\) is the side of square. 

Or  \(2[r+\sqrt 3 r\)+\(\sqrt 2 r] \) =\(\sqrt 2 a\)

Or \(r =\frac{{\sqrt 2 a}}{{2(1 + \sqrt 3  + \sqrt 2 )}}\)= \(\frac{a}{{\sqrt 2 (1 + \sqrt 3  + \sqrt 2 )}}\)