Geometry
Circle
Properties of circle
- Any perpendicular from the centre bisects a chord and any line which bisects a chord and passing through the centre of a circle is perpendicular to the chord.
- Equal chords are equidistance from the centre and vice versa.
- Equal chords subtend equal angle at the centre of any circle.
- Angle subtended by any chord at the centre is double the angle subtended at the circumference on the same side.
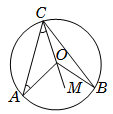
In this diagram, \(O\) is the centre
\(OA = OC =\) radius, hence \(\angle CAO = \angle OCA\)
And the \(\angle AOM\) is exterior angle of \(\angle CAO\,\,\,and\,\,\,\angle OCA\)
Hence \(\angle AOM=2\) (\(\angle ACO\)), as
\(\angle CAO = \angle OCA\), similarly
Hence \(\angle BOM= 2\) (\(\angle BCO\)), as
\(\angle CBO = \angle OCB\) and \(\angle AOB = 2\) (\(\angle ACB\))
- Angle subtended by diameter at any point of circumference is always 90°, converse of the statement is also true, which means, if angle subtended by any chord on the circumference is 90°, the chord has to be the diameter.
- If \(PAB\) and \(PCD\) are two secants lines then
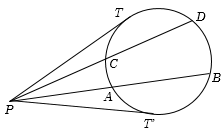
If \(PAB\) and \(PCD\) are two secants then
\(PA.PB = PC.PD\)
A line that touches the circle at only one point is a tangent to the circle \(PT\) is a tangent
\(PA.PB{\rm{ }} = {\rm{ }}PC.PD{\rm{ }} = {\rm{ }}P{T^2}\).
Two tangents can be drawn to the circle from any point outside the circle and these two tangents are equal in length \(P\) is the external point and the two tangents \(PT\) and \(PT\)’ are equal.
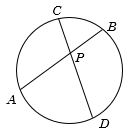
If the point \(P\) is inside the circle, then again the same rule can be applied,
In the above diagram \(PA.PB = PC.PD\)
In a circle if \(P\) is an external point and \(PAB\) and \(PCD\) are two secant lines, then the angle \(APC\),
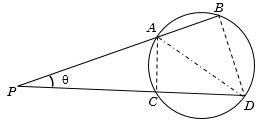
\(\theta = \frac{1}{2}\left( {{\rm{m(arc BD) - m(arc AC)}}} \right)\)
where \(m\)(arc \(BD\)) and \(m\)(arc \(AC\)) represent angles subtended by the arc \(BD\) and arc \(AC\) at the centre of the circle.
If \(P\) is inside the circle, then
\(\theta = \frac{1}{2}\left( {{\rm{m(arc BD)}} + {\rm{m(arc AC)}}} \right)\)