Geometry
Circle
Direct Common Tangent
A direct common tangent is a straight line that touches both circles on the same side. There can be two direct common tangents for two circles if one circle is not contained by the other circle. Here are some cases when two direct common tangents can be drawn to two circles.
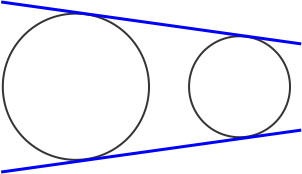
(i) Circles neither touching nor intersecting
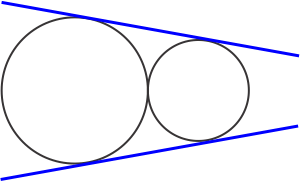
(ii) Circles touching externally
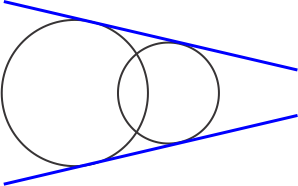
(iii) Circles intersecting
Length of Direct Common Tangent
In this diagram radii of the circles are \({r_1}\) and \({r_2}\) and distance between the centres is \(d\), The lines \(C_1P\) and \(C_2Q\) are perpendicular to \(PQ\). Draw a line perpendicular from \(C_2\) to \(C_1P\).
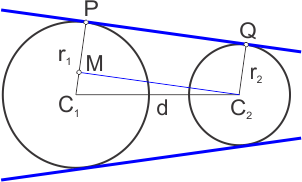
We see that \(C_1PQC_2\) is a rectangle, so the length of the tangent \(PQ =C_2M\) and \(MP =r_2\) and \(C_1M=r_1-r_2\).
Using the Pythagorean Theorem, the length of the direct common tangent\[\bbox[5px, border:1px solid blue]{C_2M = PQ = \sqrt{{d^2 - (r_1 - r_2)^2}}}\]
Properties of Direct Common Tangents
When one circle is not contained by the other circle, there are two direct common tangents to the two circles.
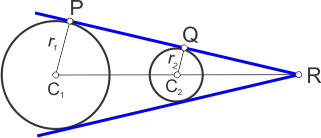
The lengths of both tangents are equal, and when we extend both tangents to meet at a point \(R\), the triangles \(\Delta {C_1}PR\) and \(\Delta {C_2}QR\) are similar.\[\bbox[5px, border:1px solid blue]{\frac{{C_1P}}{{C_1R}} = \frac{{C_2Q}}{{C_2R}}}\]
The point \(R\)divides the line \({C_1}{C_2}\)externally in the ratio of \({r_1}\) and \({r_2}\), where \({C_1}P = {r_1},\;{C_2}P = {r_2}\)
Example 01: There are two circles of radii \({r_1}\) and \({r_2}\), such that one circle touches the other externally. Find the length of the direct common tangent.
Hence length of the direct common tangent = \(\sqrt {{d^2} - {{({r_1} - {r_2})}^2}} \)
\( = \sqrt {{{({r_1} + {r_2})}^2} - {{({r_1} - {r_2})}^2}} = 2\sqrt {{r_1}{r_2}} \)
Example 02: There are three circles of radii \(a,\,b\) and \(c\) such that circles with radii \(a,\;b\) touch each other externally and circle with radius \(c\) touches both the circles
externally and all the three circles have a direct common tangent. Find the relation in \(a,\,b,\,c\)
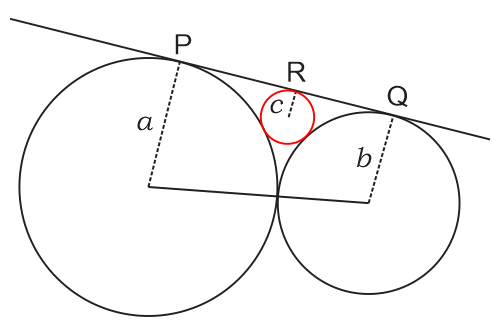
\(PQ = \sqrt {{{(a + b)}^2} - {{(a - b)}^2}} = \sqrt {4ab} \)
\(QR = \sqrt {{{(b + c)}^2} - {{(b - c)}^2}} = \sqrt {4bc} \)
\(PR = \sqrt {{{(a + c)}^2} - {{(a - c)}^2}} = \sqrt {4ac} \)
Since \(P,\,Q,\,R\) are in the same straight line, hence
\(PR + RQ = PQ\)
\(\sqrt {4ac} + \sqrt {4bc} = \sqrt {4ab} \)
\( \Rightarrow \sqrt {ac} + \sqrt {bc} = \sqrt {ab} \)