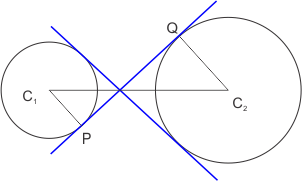
Number of Transverse Common Tangents:

There can be 2, 1, or 0 transverse common tangents, depending on the positions of the given circles. If the circles are touching externally, there will be only one transverse common tangent. However, there will be no transverse common tangents if the circles are intersecting, touching internally, or if one circle is contained by the other circle.

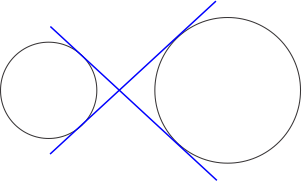
2 Transverse Common Tangents

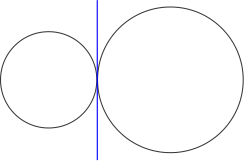
1 Transverse Common Tangent

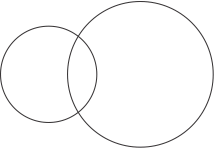
No Transverse Common Tangent

Length of the Transverse Common Tangent:

Let the radii of the two circles are \(r_1\) and \(r_2\) and the distance between their centres is \(d\). The straight line \(PQ\) is a transverse common tangent. Extend the line \(C_2Q\) to \(M\) such that \(QM=r_1\), in this way, \(PC_1MQ\) becomes a rectangle and \(C_1M=PQ\)

In the right-angled triangle \(C_1C_2M\), \[{C_1}{M^2} = {C_1}{C_2}^2 - {C_2}{M^2}\]

\[ \Rightarrow {C_1}{M^2} = {d^2} - {({r_1} + {r_2})^2}\]

Length of the Transverse Common Tangent \[PQ=C_1M =\sqrt {{d^2} - {{({r_1} + {r_2})}^2}} \]

If the circles are externally touching each other, then length of transverse common tangent becomes zero as \(d = {r_1} + {r_2}\)

Example 22: In the following diagram 3 circle are touching each other and have direct common tangent find the relation in \(‘a’, ‘b’, ‘c’,\) where \(c\) is the radius of the smallest circle. 

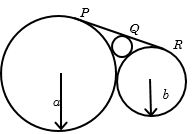
Solution: \(PQ\) is the direct common tangent for the circles whose radii are \(a\) and \(c\), and distance between the centres \(= (a + c)\)

\(PQ =\sqrt {{{(a + c)}^2} - {{(a - c)}^2}} \)=\(\sqrt {4ac} \), similarly

\(QR=\sqrt {{{(b + c)}^2} - {{(b - c)}^2}} \)=\(\sqrt {4bc} \) and 

\(PR=\sqrt {{{(a + b)}^2} - {{(a - b)}^2}} \)=\(\sqrt {4ab} \)

Now \(PQ + QR = PR\), or

\(\sqrt {ac}  + \sqrt {bc}  = \sqrt {ab} \)