When we have only one equation involving two or more unknown variables, then there are infinite solutions, but with some restrictions on the variables, the number of solutions becomes limited. It is a known fact that if number of unknown quantities is greater than the number of independent equations, then there will be many solutions and the equations become indeterminate. But if the variables are positive integers, then solution to the equation becomes easier. Consider the following example. 

Suppose there is only one equation \(3x + 4y = 88\), where \(x\) and \(y\) are positive integers.

\(\Rightarrow 4y = 88 - 3x\) 

Left hand side of the equation is a multiple of 4, hence right hand side is also a multiple of 4.

Therefore \(3x\) must be a multiple of 4, so minimum value of \(x\) is 4 and corresponding value of \(y\) is 19. 

Now there will be more solutions other than (4, 19), in the solution set if \(x\) increases by 4 then \(y\) decreases by 3 or vice versa; in general \(x\) increases /decreases at the rate of coefficient of \(y\) and \(y\) decreases/increases at the rate of coefficient of  \(x\), where coefficients of \(x\) and \(y\) are co-prime to each other. The complete solution set is given below:

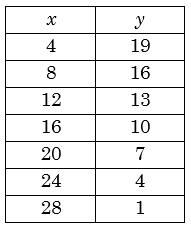
Hence total number of solutions is 7.

Note: It should be noted that series of values of \(x\) and \(y\) in the solutions of \(ax \pm by = c\) forms two Arithmetical progressions in which the common differences are \(b\) and \(a\) respectively, where \(a, b, c\) are positive integers and the equation \(ax \pm by = c\)  is in the simplest form, that means  \({\rm{HCF}}(a,b,c) = 1\).

Example 01: Solve \(3x + 5y = 38\), where \(x\) and \(y\) are positive integers. 

Solution: Re write the equation as \(3x = 38 - 5y\)

\(\Rightarrow 3x = 33 - 6y + (5 + y)\). Since \(x\) and \(y\) are positive integers, hence \(33 - 6y + (5 + y)\) must be divisible by 3, that means \((5 + y)\) is multiple of 3. 

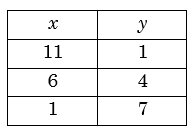
Hence minimum value of \(y\) is 1 and corresponding value of \(x\) is 11.

In order to get complete solution, values of \(x\) will change at the rate of 5, and values of \(y\) will change at the rate of 3. Since \(3x + 5y\) is a constant, thus changes in \(x\) and \(y\) will be of opposite signs.  There will be 3 solutions. 

Example 02: Solve the equation for positive integers \(17x - 15y = 50\).

Solution: \(15y = 17x – 50\)

\(\Rightarrow 15y = 15x - 45 + 2x – 5\)

\(\Rightarrow 2x – 5\) is a multiple of 15, so \(x = 10\) and corresponding value of \(y\) is 8. This general solution will be \(x = 15k + 10\), \(y = 17k + 8\). 

Number of solutions will be infinite. These solutions are obtained by assigning to \(k\) the values  0, 1, 2, 

Questions 01: Find all values of \(x\) and \(y\) if \(11x +15y = 1031\), where \(x\) and \(y\) belong to the set of natural numbers.

Questions 02: If \(775x - 711y = 1\) and \(x, y\) are natural numbers, find the least value of \(x + y\).

Test on Indeterminate Equations