This questions can be solved quickly by taking \(n = 2\), then
\(\cot {\alpha _1}\cot {\alpha _2} = 1 \Rightarrow \cot {\alpha _1} = \tan {\alpha _2}\)
\( \Rightarrow \tan \left( {\frac{\pi }{2} - {\alpha _1}} \right) = \tan {\alpha _2}\) or \({\alpha _1} + {\alpha _2} = \frac{\pi }{2}\)
Now \((\cos {\alpha _1})(\cos {\alpha _2}) = \cos {\alpha _1}\cos \left( {\frac{\pi }{2} - {\alpha _1}} \right) = \cos {\alpha _1}\sin {\alpha _1}\)
\( = \frac{{\sin 2{\alpha _1}}}{2}\), and this value is maximum when \(2{\alpha _1} = 90\) or \({\alpha _1} = 45\)
Hence the maximum value occurs at \({\alpha _1} = {\alpha _2} = 45\)
Substituting the values \({\alpha _1} = {\alpha _2} = {\alpha _3} = ......{\alpha _n} = \frac{\pi }{4}\), then maximum value of \((\cos {\alpha _1})(\cos {\alpha _2}).....(\cos {\alpha _n})\) is \({\left( {\frac{1}{{\sqrt 2 }}} \right)^n} = \frac{1}{{{2^{n/2}}}}\)
Alternate Solution: Given that \(\frac{{\cos {\alpha _1}\cos {\alpha _2}\cos {\alpha _3}......\cos {\alpha _n}}}{{\sin {\alpha _1}\sin {\alpha _2}\sin {\alpha _3}......\sin {\alpha _n}}} = 1\)
\( \Rightarrow \cos {\alpha _1}\cos {\alpha _2}\cos {\alpha _3}......\cos {\alpha _n}\)
= \(\sin {\alpha _1}\sin {\alpha _2}\sin {\alpha _3}......\sin {\alpha _n}\)
\(\Rightarrow {\left( {\cos {\alpha _1}\cos {\alpha _2}\cos {\alpha _3}......\cos {\alpha _n}} \right)^2}\)
= \(\left( {\cos {\alpha _1}\sin {\alpha _1}} \right)\left( {\cos {\alpha _2}\sin {\alpha _2}} \right)......\left( {\cos {\alpha _n}\sin {\alpha _n}} \right)\)
Using \(\cos \theta \sin \theta = \frac{{\sin 2\theta }}{2}\), we have
\({\left( {\cos {\alpha _1}\cos {\alpha _2}\cos {\alpha _3}......\cos {\alpha _n}} \right)^2} = \frac{{\left( {\sin 2{\alpha _1}} \right)\left( {\sin 2{\alpha _2}} \right)......\left( {\sin 2{\alpha _n}} \right)}}{{{2^n}}}\)
As maximum values of \(\sin 2\alpha_1 = \sin 2{\alpha _2} = .... = 1\), hence
\({\left( {\cos {\alpha _1}\cos {\alpha _2}\cos {\alpha _3}......\cos {\alpha _n}} \right)^2} \le \frac{1}{{{2^n}}}\)

We know that
\((1 + \tan \theta )[1 + \tan (45 - \theta )] = (1 + \tan \theta )\left( {1 + \frac{{\tan 45 - \tan \theta }}{{1 + \tan 45\tan \theta }}} \right)\)
\( = (1 + \tan \theta )\left( {\frac{{1 + \tan \theta + 1 - \tan \theta }}{{1 + \tan \theta }}} \right) = 2\)
\( \Rightarrow (1 + \tan {1^ \circ })(1 + \tan {44^ \circ }) = (1 + \tan {2^ \circ })(1 + \tan {43^ \circ }).. = 2\)
Hence the value of \(n = 23\).

We know that \(\sin \theta \cdot \sin (60 - \theta ) \cdot \sin (60 + \theta ) = \frac{{\sin 3\theta }}{4}\)
The expression in the question can be written as
\(\sin 12\sin 48\sin 54 = \frac{{\sin 12\sin 48\sin 72\sin 54}}{{\sin 72}}\)
\( = \frac{{\sin 36\sin 54}}{{4\sin 72}} = \frac{{2\sin 36\sin 54}}{{8\sin 72}}\)
\(\frac{{\sin 72}}{{8\sin 72}} = \frac{1}{8} = {\sin ^3}30\)

Given that \(2\cos \left( {\cfrac{{\alpha + \beta }}{2}} \right)\cos \left( {\cfrac{{\alpha - \beta }}{2}} \right) = a\)
\(2\sin \left( {\cfrac{{\alpha + \beta }}{2}} \right)\cos \left( {\cfrac{{\alpha - \beta }}{2}} \right) = b\)
Dividing second equation be first, we get
\(\cfrac{{\sin \left( {\cfrac{{\alpha + \beta }}{2}} \right)}}{{\cos \left( {\cfrac{{\alpha + \beta }}{2}} \right)}} = \cfrac{b}{a} \Rightarrow \tan \left( {\cfrac{{\alpha + \beta }}{2}} \right) = \cfrac{b}{a}\)
Using the formula,
\(\sin 2\theta = \cfrac{{2\tan \theta }}{{1 + {{\tan }^2}\theta }},\;\;\cos 2\theta = \cfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}\)
\(\sin 2\theta + \cos 2\theta = \cfrac{{2\tan \theta + 1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}\)
\( = \cfrac{{\cfrac{{2b}}{a} + 1 - \cfrac{{{b^2}}}{{{a^2}}}}}{{1 + \cfrac{{{b^2}}}{{{a^2}}}}} = \cfrac{{{a^2} + 2ab - {b^2}}}{{{a^2} + {b^2}}}\)

\(A = 1 - {\sin ^2}\theta + {\sin ^4}\theta = 1 - {\sin ^2}\theta (1 - {\sin ^2}\theta )\)
\( \Rightarrow A = 1 - {\sin ^2}\theta {\cos ^2}\theta \)
\( \Rightarrow A = 1 - \frac{{{{\sin }^2}2\theta }}{4}\)
Since, \(0 \le {\sin ^2}2\theta \le 1\), hence \(\frac{3}{4} \le A \le 1\)

Adding 1 and subtracting 1,
\(\cfrac{{\sqrt 3 \cos 20}}{{\sin 20}} - 1 + 1 - 4\cos 20\)
\( = \cfrac{{\sqrt 3 \cos 20 - \sin 20}}{{\sin 20}} + 1 - 4\cos 20\)
\( = \cfrac{{2\left( {\cfrac{{\sqrt 3 }}{2}\cos 20 - \cfrac{1}{2}\sin 20} \right)}}{{\sin 20}} + 1 - 4\cos 20\)
\( = \cfrac{{2(\sin 60\cos 20 - \cos 60\sin 20)}}{{\sin 20}} + 1 - 4\cos 20\)
\( = \cfrac{{2\sin 40}}{{\sin 20}} + 1 - 4\cos 20 = 4\cos 20 + 1 - 4\cos 20\) = 1

Using the formula,
\(\sin 2\theta = \cfrac{{2\tan \theta }}{{1 + {{\tan }^2}\theta }},\;\;\cos 2\theta = \cfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}\)
\(a\cos 2\theta + b\sin 2\theta = a\left( {\cfrac{{1 - \cfrac{{{b^2}}}{{{a^2}}}}}{{1 + \cfrac{{{b^2}}}{{{a^2}}}}}} \right) + b\left( {\cfrac{{2\cfrac{b}{a}}}{{1 + \cfrac{{{b^2}}}{{{a^2}}}}}} \right)\)
\( = a\left( {\cfrac{{{a^2} - {b^2} + 2{b^2}}}{{{a^2} + {b^2}}}} \right) = a\)

We know that \(\cos 2\theta = \cfrac{{1 - {{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}\)
Hence \(\cfrac{{1 - {{\tan }^2}15^\circ }}{{1 + {{\tan }^2}15^\circ }} = \cos 30 = \cfrac{{\sqrt 3 }}{2}\)

Given that \(\sin x,\;\cos x,\;\tan x\)are in GP, then
\({\cos ^2}x = \sin x \cdot \tan x \Rightarrow {\cos ^3}x = {\sin ^2}x\)
Or \({\cot ^3}x = \frac{1}{{\sin x}} = {\rm{cosec}}\,x\)
\( \Rightarrow {\cot ^6}x = {\rm{cosec}}{\,^2}x\)
Therefore \({\cot ^6}x - {\cot ^2}x = {\rm{cose}}{{\rm{c}}^2}x - {\cot ^2}x = 1\)

\(\sin 30\cos 45 + \cos 30\sin 45 = \frac{1}{2} \times \frac{1}{{\sqrt 2 }} + \frac{{\sqrt 3 }}{2} \times \frac{1}{{\sqrt 2 }}\)
\( = \frac{{\sqrt 3 + 1}}{{2\sqrt 2 }}\)

Given that \(A - B = \cfrac{\pi }{4}\)
\( \Rightarrow \tan (A - B) = \tan \cfrac{\pi }{4}\)
\( \Rightarrow \cfrac{{\tan A - \tan B}}{{1 + \tan A\tan B}} = 1\)
or tan A – tan B = 1 + tan A tan B
or tan A – tan B – tan A tan B = 1
Adding 1 on both sides
(1+ tan A) – tan B(1 + tan A) = 2
(1+ tan A)(1– tan B) = 2

We know that 1 radian is approximately 57°. Clearly sin 1 > sin 1°.

Given that \(\cos (\alpha + \beta ) = \cfrac{4}{5}\) and \(\sin (\alpha - \beta ) = \cfrac{5}{{13}}\)
Thus \(\tan (\alpha + \beta ) = \cfrac{3}{4}\) and \(\tan (\alpha - \beta ) = \cfrac{5}{{12}}\)
Now \(\tan 2\alpha = \tan \left( {\left( {\alpha + \beta } \right) + \left( {\alpha - \beta } \right)} \right)\)
\( = \cfrac{{\tan \left( {\alpha + \beta } \right) + \tan \left( {\alpha - \beta } \right)}}{{1 - \tan \left( {\alpha + \beta } \right)\,\tan \left( {\alpha - \beta } \right)}}\)
\( = \cfrac{{\cfrac{3}{4} + \cfrac{5}{{12}}}}{{1 - \cfrac{3}{4} \times \cfrac{5}{{12}}}} = \cfrac{{\cfrac{{27 + 15}}{{36}}}}{{1 - \cfrac{5}{{16}}}} = \cfrac{{\cfrac{{42}}{{36}}}}{{\cfrac{{11}}{{16}}}} = \cfrac{{56}}{{33}}\)

From the give equation,
\(1 - {\cos ^2}x = 1 - \sin x\)or \({\cos ^2}x = \sin x\)
Squaring it again we get the answer
\({\cos ^4}x = 1 - {\cos ^2}x\)\( \Rightarrow {\cos ^4}x + {\cos ^2}x = 1\).
(This question is again repeated in NIMCET 2013)

Given that \(\sin (\pi \cos \theta ) = \cos (\pi \sin \theta )\)
\( \Rightarrow \sin (\pi \cos \theta ) = \sin \left( {\frac{\pi }{2} \pm \pi \sin \theta } \right)\)
\( \Rightarrow \pi \cos \theta = \frac{\pi }{2} \pm \pi \sin \theta \)
\( \Rightarrow \cos \theta \mp \sin \theta = \frac{1}{2}\)
Squaring both the sides,
\({\cos ^2}\theta + {\sin ^2}\theta \pm 2\sin \theta \cos \theta = \frac{1}{4}\)
or \(\sin 2\theta = \pm \frac{3}{4}\)

Given that \(\sin x + a\cos x = b\), let \(a\sin x - \cos x = y\), squaring and adding both the equations,
\({(\sin x + a\cos x)^2} + {(a\sin x - \cos x)^2} = {b^2} + {y^2}\)
\( \Rightarrow {y^2} = 1 + {a^2} - {b^2}\) or \(|y|\, = \sqrt {{a^2} - {b^2} + 1} \)
(This question is again asked in NIMCET 2014)

This type of questions can be solved by putting a simple and suitable values of \(\theta \) both in the question and the answer choices. Here we can \(\theta = 0\) and the value of the expression in the question becomes infinity, in the choices except choice (1), all other choices are finite numbers, hence choice (1) is correct. Detailed solution is given below:
Subtracting and adding \(\cot \theta \), we have
\((\tan \theta - \cot \theta ) + 2\tan 2\theta + 4\tan 4\theta + 8\cot 8\theta + \cot \theta \)
Let us first simplify \(\tan \theta - \cot \theta \) as \(\frac{{\sin \theta }}{{\cos \theta }} - \frac{{\cos \theta }}{{\sin \theta }} = - \frac{{{{\cos }^2}\theta - {{\sin }^2}\theta }}{{\sin \theta \cos \theta }}\)
\( = \frac{{ - \cos 2\theta }}{{\frac{{\sin 2\theta }}{2}}} = - 2\cot 2\theta \)
Hence \(\tan \theta - \cot \theta = - 2\cot 2\theta \), in the same manner,
\(2\tan 2\theta - 2\cot 2\theta = - 4\cot 4\theta \) and so on.
Proceeding in the same manner, we get the value of the expression as \(\cot \theta \).

\(\tan (\alpha + \beta ) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }}\)
\( = \frac{{\frac{m}{{m + 1}} + \frac{1}{{2m + 1}}}}{{1 - \left( {\frac{m}{{m + 1}}} \right)\left( {\frac{1}{{2m + 1}}} \right)}} = \frac{{2{m^2} + 2m + 1}}{{2{m^2} + 2m + 1}} = 1\)
\( \Rightarrow \alpha + \beta = \frac{\pi }{4}\)

We know that \(\sin \theta \sin (60 - \theta )\sin (60 + \theta ) = \cfrac{{\sin 3\theta }}{4}\)
\( \Rightarrow \sin 20\sin 40\sin 80 = \frac{{\sin (3 \times 20)}}{4} = \frac{{\sqrt 3 }}{8}\)

\(\cot B - \cot A = \cfrac{{\tan A - \tan B}}{{\tan A\tan B}} = y\)
Putting the value of \(\tan A - \tan B\), we get
\(\tan A\tan B = \frac{x}{y}\)
Now \(\tan (A - B) = \cfrac{{\tan A - \tan B}}{{1 + \tan A\tan B}} = \frac{x}{{1 + \frac{x}{y}}} = \frac{{xy}}{{x + y}}\)
Hence \(\cot (A - B) = \frac{{x + y}}{{xy}} = \frac{1}{x} + \frac{1}{y}\)

We know that tan (90 – x) = cot x, hence
tan 89° = tan(90° – 1) = cot 1°
Hence tan 1°. tan 89° = 1, tan 2°. tan 88° = 1 etc.
Except tan 45°, all the terms can be paired, hence the answer is 1.

We know that \({\sin ^2}\theta + {\cos ^2}\theta = 1\), if we use higher powers of \(\sin \theta \) and \(\cos \theta \), then the answer will be less than or equal to 1. Also \(\sin \theta \) and \(\cos \theta \) are not simultaneously zero, thus \(0 < {\sin ^{20}}\theta + {\cos ^{48}}\theta \le 1\)

Since \(\tan \left( {\frac{{7\pi }}{8}} \right) = - \tan \left( {\frac{\pi }{8}} \right)\)
Let is first calculate the value of \(\tan \left( {\frac{\pi }{8}} \right)\), using the formula \(\cos 2\theta = \cfrac{{1 - {{\tan }^2}\theta }}{{1 - {{\tan }^2}\theta }}\), we have
\(\cos \cfrac{\pi }{4} = \cfrac{{1 - {{\tan }^2}\left( {\frac{\pi }{8}} \right)}}{{1 + {{\tan }^2}\left( {\frac{\pi }{8}} \right)}}\)\( \Rightarrow {\tan ^2}\cfrac{\pi }{8} = \cfrac{{\sqrt 2 - 1}}{{\sqrt 2 + 1}} = {(\sqrt 2 - 1)^2}\)
Hence \(\tan \frac{\pi }{8} = \sqrt 2 - 1\) or \(\tan \left( {\frac{{7\pi }}{8}} \right) = - \tan \left( {\frac{\pi }{8}} \right) = 1 - \sqrt 2 \)

Given \(\cos \theta = \frac{5}{{13}},\frac{{3\pi }}{2} < \theta < 2\pi \)
we know than \(\tan 2\theta = \frac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\) [\(3\pi < 2\theta < 4\pi \)]
so, \(\tan \theta = \frac{{ - 12}}{5}\)
\(\therefore \tan 2\theta = \frac{{2 \times \left( {\frac{{ - 2}}{5}} \right)}}{{1 \times {{\left( {\frac{{ - 12}}{5}} \right)}^2}}}\)= \(\frac{{120}}{{119}}\)

The expression cos 20° + cos 100° + cos 140° can be simplified as:
\( = 2\cos \left( {\frac{{20 + 100}}{2}} \right)\cos \left( {\frac{{100 - 20}}{2}} \right) + \cos 140\)
\( = 2\cos 60\cos 40 + \cos 140\)
\( = \cos 40 + \cos 140\)
\( = \cos 40 + \cos (180 - 40) = 0\)

Given that \(\tan x = \frac{{ - 3}}{4}\) and \(\frac{{3\pi }}{2} < x < 2\pi \)
means \(x\) lies in fourth quadrant
Then \(\sin x = - \frac{3}{5}\) and \(\cos x = \frac{4}{5}\)
Now \(\sin 2x = 2\sin x\cos x\)
\(\sin 2x = - 2 \times \frac{3}{5} \times \frac{4}{5} = - \frac{{24}}{{25}}\)

Given that \(\cos \theta = \frac{4}{5},\;\cos \varphi \frac{{12}}{{13}}\)
Given that \(\theta \), and \(\phi \)both lies in fourth quadrant then
\(\sin \theta = \frac{{ - 3}}{5}\) and \(\sin \phi = \frac{{ - 5}}{{13}}\)
Now, \(\cos (\theta + \phi ) = \cos \theta \cos \phi - \sin \theta \sin \phi \)
= \(\frac{4}{5} \times \frac{{12}}{{13}} - \left( {\frac{{ - 3}}{5}} \right)\left( {\frac{{ - 5}}{{13}}} \right)\)
= \(\frac{{48}}{{65}} - \frac{{15}}{{65}} = \frac{{33}}{{65}}\)

It is a standard result, the value is \(\frac{{\sqrt {10 - 2\sqrt 5 } }}{4}\). This question can one by eliminating the choice. As sin 36° lies between sin 30° and sin 45°, so the answer is more than \(\frac{1}{2}\) and less than \(\frac{1}{{\sqrt 2 }}\). Only choice (2) is in this range.

\(\cos C - \cos D = 2\sin \left( {\frac{{C + D}}{2}} \right)\sin \left( {\frac{{D - C}}{2}} \right)\)
\(\cos 5x - \cos 7x = 2\sin \left( {\frac{{5x + 7x}}{2}} \right)\sin \left( {\frac{{7x - 5x}}{2}} \right)\)
= \( = 2\sin 6x\sin x\)

Given \(y = 4{\sin ^2}x + 3{\cos ^2}x + \sin \,x/2 + \cos x/2\)
\( \Rightarrow y = 3 + {\sin ^2}x + \sin \,\frac{x}{2} + \cos \frac{x}{2}\)
We know that \(\sin \frac{x}{2} + \cos \frac{x}{2}\) is maximum when \(\frac{x}{2} = \frac{\pi }{4}\) or \(x = \frac{\pi }{2}\) and at \(x = \frac{\pi }{2}\), \(\sin x\) is also maximum.
So maximum value of expression is \(3 + 1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 2 }} = 4 + \sqrt 2 \)

Rewrite the equation as \(\sin (\theta + \alpha - \alpha ) = 3\sin (\theta + \alpha + \alpha )\)
\( \Rightarrow \sin (\theta + \alpha )\cos \alpha - \cos (\theta + \alpha )\sin \alpha \)
\(\;\;\;\; = 3\sin (\theta + \alpha )\cos \alpha + 3\cos (\theta + \alpha )\sin \alpha \)
Dividing by \(\cos (\theta + \alpha )\cos \alpha \), we have
\(\tan (\theta + \alpha ) - \tan \alpha = 3\tan (\theta + \alpha ) + 3\tan \alpha \)
\( \Rightarrow \tan (\theta + \alpha ) + 2\tan \alpha = 0\)

We can apply Jensen’s inequality to get,
\(\sec \left( {\frac{{A + B + C}}{3}} \right) \le \,\,\left( {\frac{{\sec A + \sec B + \sec C}}{3}} \right)\)
\( \Rightarrow \sec A + \sec B + \sec C \ge 3\sec 60\)
Hence minimum value of \(\sec A + \sec B + \sec C\) is 6.
This question can also be done just by putting A = B = C = 60°.

Suppose \(\frac{{\tan x}}{2} = \frac{{\tan y}}{3} = \frac{{\tan z}}{5} = k\), then \(\tan x = 2k,\;\tan y = 3k,\;\tan z = 5k\)
In a triangle, \(\tan x + \tan y + \tan z = \tan x\tan y\tan z\)
\( \Rightarrow 2k + 3k + 5k = (2k)(3k)(5k)\) or \(k = \pm \frac{1}{{\sqrt 3 }}\)
Now \({\tan ^2}x + {\tan ^2}y + {\tan ^2}z = (4 + 9 + 25){k^2}\)
\( = \frac{{38}}{3}\)

Using Jensen's Inequality,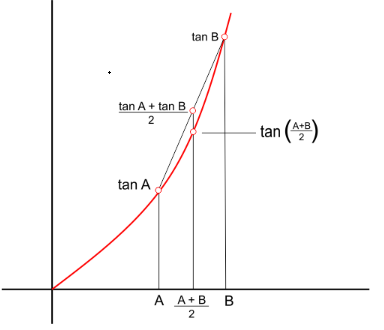

\(\tan \left( {\frac{{A + B}}{2}} \right) \le \frac{{\tan A + \tan B}}{2}\)
\( \Rightarrow \frac{{\tan A + \tan B}}{2} \ge \tan 15\)
\( \Rightarrow \tan A + \tan B \ge 2\left( {\frac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}}} \right)\)
\(\;\;\;\;\;\;\;\;\;\; \ge 2\left( {\frac{{(\sqrt 3 - 1)(\sqrt 3 - 1)}}{{(\sqrt 3 + 1)(\sqrt 3 - 1)}}} \right) \ge 4 - 2\sqrt 3 \)

Eliminating \(y\) from the given relations,
\(\cos x = \tan y = \frac{1}{{\cot y}} = \frac{1}{{\tan z}} = \cot z = \tan x\)
\( \Rightarrow \cos x = \tan x\)
Or \(\sin x = {\cos ^2}x = 1 - {\sin ^2}x\)
\( \Rightarrow \sin x = \frac{{ - 1 + \sqrt 5 }}{2}\)

\(\tan \left( {45 + \frac{\theta }{2}} \right) = \frac{{1 + \tan \frac{\theta }{2}}}{{1 - \tan \frac{\theta }{2}}}\)
\( = \frac{{\sin \frac{\theta }{2} + \cos \frac{\theta }{2}}}{{\cos \frac{\theta }{2} - \sin \frac{\theta }{2}}} = \frac{{{{\left( {\sin \frac{\theta }{2} + \cos \frac{\theta }{2}} \right)}^2}}}{{{{\cos }^2}\frac{\theta }{2} - {{\sin }^2}\frac{\theta }{2}}}\)
\( = \frac{{1 + \sin \theta }}{{\cos \theta }} = \sec \theta + \tan \theta \)

The value of \(\sin 10\sin 50\sin 70\)
\( = \frac{{\sin (3 \times 10)}}{4} = \frac{1}{8}\)
(using \(\sin \theta \sin (60 - \theta )\sin (60 + \theta ) = \frac{{\sin 3\theta }}{4}\))

The expression can be written as,
\(\frac{{{{\tan }^2}A}}{{\tan A - 1}} + \frac{{\cot A}}{{1 - \tan A}}\)
\( = \frac{1}{{\tan A - 1}}\left( {{{\tan }^2}A - \cot A} \right) = \frac{{{{\tan }^3}A - 1}}{{\tan A(\tan A - 1)}}\)
\( = \frac{{1 + {{\tan }^2}A + \tan A}}{{\tan A}} = 1 + \frac{{{{\sec }^2}A}}{{\tan A}}\)
\( = 1 + \sec A\,{\rm{cosec}}\,A\)

Using the formula, \(\sin x = \frac{{2\tan (x/2)}}{{1 + {{\tan }^2}(x/2)}}\) and \(\cos x = \frac{{1 - {{\tan }^2}(x/2)}}{{1 + {{\tan }^2}(x/2)}}\)
Let us assume \(\tan \,(x/2) = t\), then
\(3\left( {\frac{{2t}}{{1 + {t^2}}}} \right) + 4\left( {\frac{{1 - {t^2}}}{{1 + {t^2}}}} \right) = 5\)
\( \Rightarrow 9{t^2} - 6t + 1 = 0\)
Or \(6\tan (x/2) - 9{\tan ^2}(x/2) = 1\)

We can put values of the angles A, B and C to get an idea about the value of \(k\), put A = B = C = 60°,
\(k = {\tan ^2}30 + {\tan ^2}30 + {\tan ^2}30 = 1\)
Put another set of values A = B = 30° and C = 120°,
\(k = {\tan ^2}15 + {\tan ^2}15 + {\tan ^2}45 > 1\)
Hence \(k \ge 1\)

tan 9° – tan 27° – tan 63° + tan 81°
= \(\cfrac{{\sin 9^\circ }}{{\cos 9^\circ }} - \cfrac{{\sin 27^\circ }}{{\cos 27^\circ }} - \left[ {\cfrac{{\sin {{63}^ \circ }}}{{\cos {{63}^ \circ }}} - \cfrac{{\sin 81^\circ }}{{\cos 81^\circ }}} \right]\) = A – B
Where A = \(\left( {\cfrac{{\sin {9^ \circ }\cos {{27}^ \circ } - \cos {9^ \circ }\sin {{27}^ \circ }}}{{\cos {9^ \circ }\cos {{27}^ \circ }}}} \right) = \cfrac{{ - \sin {{18}^ \circ }}}{{\cos {9^ \circ }\cos {{27}^ \circ }}}\)\( = \cfrac{{ - 2\sin {9^ \circ }}}{{\cos {{27}^ \circ }}}\)
B = \(\cfrac{{\sin {{63}^ \circ }\cos {{81}^ \circ } - \sin {{81}^ \circ }\cos {{63}^ \circ }}}{{\cos {{63}^ \circ }\cos {{81}^ \circ }}}\)\( = \cfrac{{ - \sin {{18}^ \circ }}}{{\sin {{27}^ \circ }\sin {9^ \circ }}} = \cfrac{{ - 2\cos {9^ \circ }}}{{\sin {{27}^ \circ }}}\)
Hence A – B = \(\cfrac{{2\cos {9^ \circ }}}{{\sin {{27}^ \circ }}} - \cfrac{{2\sin {9^ \circ }}}{{\cos {{27}^ \circ }}}\)\( = \cfrac{{2\left( {\cos {9^ \circ }\cos {{27}^ \circ } - \sin {9^ \circ }\sin {{27}^ \circ }} \right)}}{{\sin {{27}^ \circ }\cos {{27}^ \circ }}}\)
\( = \cfrac{{2\cos {{36}^ \circ }}}{{\left( {\cfrac{{\sin {{54}^ \circ }}}{2}} \right)}} = \cfrac{{4\cos {{36}^ \circ }}}{{\sin {{54}^ \circ }}}\) = 4.

We know that \({\rm{cose}}{{\rm{c}}^2}\,\theta - {\cot ^2}\theta = 1\)
Hence \(({\rm{cosec}}\,\theta + \cot \theta )({\rm{cosec}}\,\theta - \cot \theta ) = 1\)
Given that \({\rm{cosec}}\,\theta - \cot \theta = 2\)
\( \Rightarrow {\rm{cosec}}\,\theta + \cot \theta = \frac{1}{{{\rm{cosec}}\,\theta - \cot \theta }} = \frac{1}{2}\)
Adding the two equations, we have
\(2{\rm{cosec}}\,\theta = 2 + \frac{1}{2} \Rightarrow \color{blue}{{\rm{cosec}}\,\theta = \frac{5}{4}}\)

Sum of the roots \(\tan 30 + \tan 15 = - p\) and
product of the roots \(\tan 30 \cdot \tan 15 = q\)
We know that \([1 + \tan \theta ][1 + \tan (45 - \theta )] = 2\)
\( \Rightarrow (1 + \tan 30)(1 + \tan 15) = 2\)
\( \Rightarrow 1 + \tan 30 + \tan 15 + \tan 30 \cdot \tan 15 = 2\)
Or \(1 - p + q = 2\)
\( \color{blue}{\Rightarrow 2 + p - q = 1}\)

Given that \(\left( {\tan {\alpha _1}} \right)\left( {\tan {\alpha _2}} \right).....\,\left( {\tan {\alpha _n}} \right) = 1\)
\( \Rightarrow \sin {\alpha _1}\sin {\alpha _2}.....\sin {\alpha _n} = \cos {\alpha _1}\cos {\alpha _2}....\cos {\alpha _n}\)
Multiplying by \(\sin {\alpha _1}\sin {\alpha _2}....\sin {\alpha _n}\) both sides,
\({\left( {\sin {\alpha _1}\sin {\alpha _2}.....\sin {\alpha _n}} \right)^2} = \left( {\sin {\alpha _1}\cos {\alpha _1}} \right)\left( {\sin {\alpha _2}\cos {\alpha _2}} \right)....\)
\( \Rightarrow {\left( {\sin {\alpha _1}\sin {\alpha _2}.....\sin {\alpha _n}} \right)^2} = \frac{1}{{{2^n}}}\left( {\sin 2{\alpha _1}} \right)\left( {\sin 2{\alpha _2}} \right)....\)
The value will be maximum at \({\alpha _1} = {\alpha _2} = .....\, = {\alpha _n} = \frac{\pi }{4}\)
Hence maximum value is \(\sqrt {\frac{1}{{{2^n}}}} = \frac{1}{{{2^{n/2}}}}\)

The given expression can be written as
\(\frac{{1 + \cos 2\theta }}{2} - 3\sin 2\theta + \frac{3}{2}\left( {1 - \cos 2\theta } \right) + 2\)
\( = - 3\sin 2\theta - \cos 2\theta + 4\)
Hence maximum value = \(4 + \sqrt {{{( - 3)}^2} + {{( - 1)}^2}} = 4 + \sqrt {10} \)