\({\sec ^{ - 1}}\left( {\frac{{x + 1}}{{x - 1}}} \right) = {\cos ^{ - 1}}\left( {\frac{{x - 1}}{{x + 1}}} \right)\)
Now y =\({\sec ^{ - 1}}\left( {\frac{{x + 1}}{{x - 1}}} \right) + {\sin ^{ - 1}}\left( {\frac{{x - 1}}{{x + 1}}} \right)\)
= \({\cos ^{ - 1}}\left( {\frac{{x - 1}}{{x + 1}}} \right) + {\sin ^{ - 1}}\left( {\frac{{x - 1}}{{x + 1}}} \right) = \pi /2\)
Hence \(dy/dx = 0\)

\({\tan ^{ - 1}}\left( {\frac{1}{{1 + 2}}} \right) = {\tan ^{ - 1}}\left( {\frac{{2 - 1}}{{1 + 1 \times 2}}} \right) = {\tan ^{ - 1}}2 - {\tan ^{ - 1}}1\)
\({\tan ^{ - 1}}\left( {\frac{1}{{1 + 2 \times 3}}} \right) = {\tan ^{ - 1}}\left( {\frac{{3 - 2}}{{1 + 2 \times 3}}} \right) = {\tan ^{ - 1}}3 - {\tan ^{ - 1}}2\)
Writing all the terms in this manner, we have the last term as
\({\tan ^{ - 1}}\left( {\frac{1}{{1 + n(n + 1)}}} \right) = {\tan ^{ - 1}}\left( {\frac{{(n + 1) - n}}{{1 + n(n + 1)}}} \right) = {\tan ^{ - 1}}(n + 1) - {\tan ^{ - 1}}n\)
Adding all the terms, we get the required sum as
\({\tan ^{ - 1}}(n + 1) - {\tan ^{ - 1}}1 = {\tan ^{ - 1}}\left( {\frac{n}{{n + 2}}} \right)\)

\({\sin ^{ - 1}}x + \frac{\pi }{2} - {\sin ^{ - 1}}(1 - x) = - {\sin ^{ - 1}}x\)
\( \Rightarrow {\sin ^{ - 1}}(1 - x) = \frac{\pi }{2} + 2{\sin ^{ - 1}}x\)
Let \({\sin ^{ - 1}}x = \theta \), then \({\sin ^{ - 1}}(1 - x) = \frac{\pi }{2} - 2\theta \)
\( \Rightarrow 1 - x = \sin \left( {\frac{\pi }{2} - 2\theta } \right)\)
Or \(1 - x = \cos 2\theta = 1 - 2{\sin ^2}\theta \)
Hence \(1 - x = 1 - 2{x^2} \Rightarrow 2{x^2} - x = 0\)

\({\tan ^{ - 1}}\left( {\frac{{2x + 3x}}{{1 - 6{x^2}}}} \right) = \frac{\pi }{4}\)
\( \Rightarrow \frac{{5x}}{{1 - 6{x^2}}} = 1\) or \(6{x^2} + 5x - 1 = 0 \Rightarrow (6x - 1)(x + 1) = 0\)
\( \Rightarrow x = \frac{1}{6}\). Another roots \(x = - 1\) does not satisfy the equation.

\(\alpha = - ({\sin ^4}x + {\cos ^4}x + \sin 2x)\)
\( \Rightarrow \alpha = - \left( {{{({{\sin }^2}x + {{\cos }^2}x)}^2} - 2{{\sin }^2}x{{\cos }^2}x + \sin 2x} \right)\)
\( \Rightarrow \alpha = - \left( {1 - \frac{{{{\sin }^2}2x}}{2} + \sin 2x} \right)\)
\( \Rightarrow \alpha = \frac{1}{2}{\left( {\sin 2x - 1} \right)^2} - \frac{3}{2}\)
The maximum and minimum values of \({(\sin 2x - 1)^2}\)can be 4 and 0, hence \( - \frac{3}{2} \le \alpha \le \frac{1}{2}\)

\({\tan ^{ - 1}}\sqrt {x(x + 1)} = \frac{\pi }{2} - {\sin ^{ - 1}}\sqrt {{x^2} + x + 1} \)
\( \Rightarrow {\tan ^{ - 1}}\sqrt {x(x + 1)} = {\cos ^{ - 1}}(\sqrt {{x^2} + x + 1} )\)
Put \(x(x + 1) = y\), then
\({\tan ^{ - 1}}\sqrt y = {\cos ^{ - 1}}\sqrt {y + 1} = {\sec ^{ - 1}}\left( {\frac{1}{{\sqrt {y + 1} }}} \right)\)
Using \({\sec ^2}\theta = 1 + {\tan ^2}\theta \), we have
\(\frac{1}{{y + 1}} - 1 = y \Rightarrow y = 0,\, - 2\)
And the corresponding real values of \(x = 0,\, - 1\)

The given equation is,
\(2{\tan ^{ - 1}}a - 2{\tan ^{ - 1}}b = 2{\tan ^{ - 1}}x\)
\( \Rightarrow 2{\tan ^{ - 1}}\left( {\frac{{a - b}}{{1 + ab}}} \right) = 2{\tan ^{ - 1}}x\) or \(x = \frac{{a - b}}{{1 + ab}}\)

The maximum value of \(\sqrt 3 \cos x + \sin x\) is \(\sqrt {3 + 1} = 2\), hence there is no solution for the equation\(\sqrt 3 \cos x + \sin x = 3\).

The equation \(2{\sin ^2}\theta - 3\sin \theta - 2 = 0\) can be factorized as \((2\sin \theta + 1)(\sin \theta - 2) = 0\)
Since \(\sin \theta \le 1\), hence \(\sin \theta = - \frac{1}{2}\)
Hence general value of \(\theta \)is, \(n\pi + {( - 1)^n}\frac{{7\pi }}{6}\)

The given expression can be written as
\({\tan ^{ - 1}}\left( {\frac{1}{{21}}} \right) + {\tan ^{ - 1}}\left( {\frac{1}{{13}}} \right) +\pi- {\tan ^{ - 1}}\left( { - \frac{1}{8}} \right)\)
= \({\tan ^{ - 1}}\left( {\frac{{\frac{1}{{21}} + \frac{1}{{13}}}}{{1 - \frac{1}{{21}} \times \frac{1}{{13}}}}} \right) +\pi- {\tan ^{ - 1}}\left( { - \frac{1}{8}} \right)\)
= \({\tan ^{ - 1}}\left( {\frac{{34}}{{272}}} \right) + \pi-{\tan ^{ - 1}}\left( { - \frac{1}{8}} \right)\)
=\({\tan ^{ - 1}}\left( {\frac{1}{8}} \right) + \pi-{\tan ^{ - 1}}\left( { - \frac{1}{8}} \right)= \pi \)

The discriminant,
\(D = {(\cos p)^2} - 4(\cos p - 1)(\sin p)\)
Since \((\cos p - 1) \le 0\), hence to make D a non-negative number, \(\sin p \le 0\)
Hence \(p \in \left( {\frac{{ - \pi }}{2},\frac{\pi }{2}} \right)\)

Given that,
\(\sin x + 1 = \cos x\)
¬\( \Rightarrow \cos x - \sin x = 1\)
\( \Rightarrow \frac{1}{{\sqrt 2 }}\cos x - \frac{1}{{\sqrt 2 }}\sin x = \frac{1}{{\sqrt 2 }}\)
\( \Rightarrow \cos \frac{\pi }{4}\cos x - \sin \frac{\pi }{4}\sin x = \cos \frac{\pi }{4}\)
\( \Rightarrow \cos \left( {\frac{\pi }{4} + x} \right) = \cos \frac{\pi }{4}\)
\( \Rightarrow \frac{\pi }{4} + x = 2n\pi \)
\(\frac{\pi }{4} + x = 2n\pi \pm \frac{\pi }{4}\)
Taking positive and negative signs, we have \(x = 2n\pi ,\;\,2n\pi - \frac{\pi }{2}\)
Now putting \(n = 0,\,1\), we get two values of \(x = 0,\,\;\frac{{3\pi }}{2}\)

Squaring the equation, we have
\({\sin ^2}x + {\cos ^2}x + 2\sin x\cos x = \frac{1}{4}\)
\( \Rightarrow 1 + \sin 2x = \frac{1}{4}\)
\( \Rightarrow 1 + \frac{{2\tan x}}{{1 - {{\tan }^2}x}} = \frac{1}{4}\)
\( \Rightarrow 3{\tan ^2}x + 8\tan x + 3 = 0\)
Hence \(\tan x = \frac{{ - 4 \pm \sqrt 7 }}{3}\)

\({\sin ^{ - 1}}\frac{1}{{\sqrt 2 }} = {\sin ^{ - 1}}\left( {\frac{1}{{\sqrt 2 }}} \right) = \frac{\pi }{4}\)
General term of the series is, \({\sin ^{ - 1}}\left( {\frac{{\sqrt n - \sqrt {n - 1} }}{{\sqrt n \sqrt {n + 1} }}} \right)\) and this term is actually equal to \({\sin ^{ - 1}}\left( {\frac{1}{{\sqrt n }}} \right) - {\sin ^{ - 1}}\left( {\frac{1}{{\sqrt {n + 1} }}} \right)\).
Hence the series can be written as
\({\sin ^{ - 1}}\frac{1}{{\sqrt 2 }} + \left( {{{\sin }^{ - 1}}\frac{1}{{\sqrt 2 }} - {{\sin }^{ - 1}}\frac{1}{{\sqrt 3 }}} \right) + \left( {{{\sin }^{ - 1}}\frac{1}{{\sqrt 3 }} - {{\sin }^{ - 1}}\frac{1}{{\sqrt 4 }}} \right) + ....\)
=\({\sin ^{ - 1}}\frac{1}{{\sqrt 2 }} + {\sin ^{ - 1}}\frac{1}{{\sqrt 2 }} = \frac{\pi }{2}\)

Given that \(y(x)\, = \,{x^2} - x\,\,\sin x - \cos x = 0\)
Differentiate the equation,
\(y'(x) = 2x - \sin x - x\cos x + \sin x\)
\( \Rightarrow \,y'(x)\, = \,x(2 - \cos x)\)
when \(x\) is positive \(y\) increases and when \(x\) is negative it decreases, thus at \(x = 0,\,\,y\) is minimum.
At \(x = 0,\,\,y = - 1\).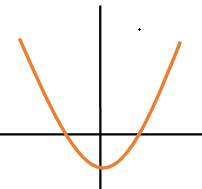

Therefore, the graph will intersect twice.

Given that sin–1 \(\frac{{2a}}{{1 + {a^2}}} + {\sin ^{ - 1}}\frac{{2b}}{{1 + {b^2}}} = 2{\tan ^{ - 1}}n\)
it can be written as
\(2{\tan ^{ - 1}}a + 2{\tan ^{ - 1}}b = 2{\tan ^{ - 1}}n\)
\( \Rightarrow {\tan ^{ - 1}}a + {\tan ^{ - 1}}b = {\tan ^{ - 1}}n\)
\( \Rightarrow {\tan ^{ - 1}}\left( {\frac{{a + b}}{{1 - ab}}} \right) = {\tan ^{ - 1}}(n)\)
Hence \(n = \frac{{a + b}}{{1 - ab}}\)

Given that \(a\sin A + b\cos A = c\)
Divide the equation by \(\sqrt {{a^2} + {b^2}} \)
\(\frac{a}{{\sqrt {{a^2} + {b^2}} }}\sin A\, + \,\frac{b}{{\sqrt {{a^2} + {b^2}} }}\cos A\, = \,\frac{c}{{\sqrt {{a^2} + {b^2}} }}\),
let \(\frac{a}{{\sqrt {{a^2} + {b^2}} }}\, = \,\sin \alpha \) then \(\frac{b}{{\sqrt {{a^2} + {b^2}} }}\, = \,\cos \alpha \)
\(\cos \left( {A - \alpha } \right)\, = \,\frac{c}{{\sqrt {{a^2} + {b^2}} }}\)\( \Rightarrow \,A\, = \,{\tan ^{ - 1}}\left( {\frac{a}{b}} \right) \pm {\cos ^{ - 1}}\left( {\frac{c}{{\sqrt {{a^2} + {b^2}} }}} \right)\)

We know that \({\cot ^{ - 1}}( - x) = \pi - {\cot ^{ - 1}}x\)
Therefore cot–1\({\cot ^{ - 1}}( - \sqrt 3 ) = \pi - {\cot ^{ - 1}}(\sqrt 3 )\)
\( = \pi - \frac{\pi }{6}\, = \,\frac{{5\pi }}{6}\)

The given equation is,
\(2\sin 3x\cos 2x = \sin 3x\)
\( \Rightarrow \sin 3x(2\cos 2x - 1) = 0\)
Hence either \(\sin 3x = 0\) or \(\cos 2x = \frac{1}{2}\)
General solutions are \(3x = n\pi ,\;\,2x = 2n\pi \pm \frac{\pi }{3}\)
Putting values of \(n,\)we get the following values of \(x\)
\(0,\,\,\frac{\pi }{3},\,\,\frac{{2\pi }}{3},\,\,\pi ,\,\,\frac{\pi }{6},\,\,\frac{{5\pi }}{6}\), there are 6 solutions.

\({\rm{cose}}{{\rm{c}}^{ - 1}}\frac{5}{3} = {\tan ^{ - 1}}\frac{3}{4}\)
\( \Rightarrow {\rm{cose}}{{\rm{c}}^{ - 1}}\frac{5}{3} + {\tan ^{ - 1}}\frac{2}{3} = {\rm{ta}}{{\rm{n}}^{ - 1}}\frac{3}{4} + {\tan ^{ - 1}}\frac{2}{3}\)
\( = {\tan ^{ - 1}}\left( {\frac{{\frac{3}{4} + \frac{2}{3}}}{{1 - \frac{3}{4} \times \frac{2}{3}}}} \right) = {\tan ^{ - 1}}\left( {\frac{{17}}{6}} \right) = {\cot ^{ - 1}}\left( {\frac{6}{{17}}} \right)\)
Hence \(\cot \left( {{\rm{cose}}{{\rm{c}}^{ - 1}}\frac{5}{3} + {{\tan }^{ - 1}}\frac{2}{3}} \right) = \cot \left( {{{\cot }^{ - 1}}\frac{6}{{17}}} \right) = \frac{6}{{17}}\)

Multiplying by \(\sin x\cos x\),
\({\sin ^4}x + {\cos ^4}x - \sin 2x(\sin x\cos x)\)
\(\;\;\;\;\;\;\;\;\;\; = \sin x\cos x + {\sin ^2}x + {\cos ^2}x\)
\( \Rightarrow {({\sin ^2}x + {\cos ^2}x)^2} - 2{\sin ^2}x{\cos ^2}x - \sin 2x(\sin x\cos x)\)
\(\;\;\;\;\;\;\;\;\;\; = \sin x\cos x + {\sin ^2}x + {\cos ^2}x\)
\( \Rightarrow 1 - \frac{{{{\sin }^2}2x}}{2} - \frac{{{{\sin }^2}2x}}{2} = \frac{{\sin 2x}}{2} + 1\)
\( \Rightarrow \sin 2x = 0\) or \(\sin 2x = - \frac{1}{2}\)
The solution of \(\sin 2x = 0\)is \(x = \frac{{n\pi }}{2}\)but this does not satisfy the give equation as either \(\tan x\) or \(\cot x\) or \(\tan x\) becomes undefined.
Hence \(\sin 2x = - \frac{1}{2}\) and \(2x = \pi + \frac{\pi }{6},\;2\pi - \frac{\pi }{6}\)
Thus \(x = \frac{{7\pi }}{{12}},\;\frac{{11\pi }}{{12}}\)

We know that \(a + \frac{1}{a} \ge 2\), when \(a > 0\), hence \({5^x} + {5^{ - x}} \ge 2\).
But \( - 1 \le \sin \theta \le 1\) or \(\sin ({e^x}) \le 1\), so \(\sin ({e^x})\) will never be equal to \({5^x} + {5^{ - x}}\)and there will be no solution.

The given equation is:
\((\sin x - 2)(\sin x + 1) = 0\)
\( \Rightarrow \sin x = - 1\)
Hence \(\color{blue}{x = \frac{{3\pi }}{2}}\). None of the answer is correct.

\(2{\tan ^{ - 1}}\left( {{\rm{cosec}}({{\tan }^{ - 1}}x) - \tan ({{\cot }^{ - 1}}x)} \right)\)
\({\rm{cosec}}\,({\tan ^{ - 1}}x) = {\rm{cosec}}\left( {{\rm{cose}}{{\rm{c}}^{ - 1}}\frac{{\sqrt {1 + {x^2}} }}{x}} \right) = \frac{{\sqrt {1 + {x^2}} }}{x}\)
\(\tan ({\cot ^{ - 1}}x) = \frac{1}{x}\)
\(\begin{array}{l} \Rightarrow 2{\tan ^{ - 1}}\left( {{\rm{cosec}}({{\tan }^{ - 1}}x) - \tan ({{\cot }^{ - 1}}x)} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 2{\tan ^{ - 1}}\left( {\frac{{\sqrt {1 + {x^2}} }}{x} - \frac{1}{x}} \right)\end{array}\)
\( = 2{\tan ^{ - 1}}\left( {\frac{{\sec \theta - 1}}{{\tan \theta }}} \right) = 2{\tan ^{ - 1}}\left( {\frac{{1 - \cos \theta }}{{\sin \theta }}} \right)\)
\( = 2{\tan ^{ - 1}}\left( {\frac{{2{{\sin }^2}\frac{\theta }{2}}}{{2\sin \frac{\theta }{2}\cos \frac{\theta }{2}}}} \right) = 2{\tan ^{ - 1}}\left( {\tan \frac{\theta }{2}} \right) = \theta \)
\( = {\tan ^{ - 1}}x\)

The maximum and minimum value of \(a\cos \alpha + b\sin \alpha = \pm \sqrt {{a^2} + {b^2}} \)
Hence maximum and minimum value of \(3\cos \alpha + 4\sin \alpha = \pm 5\)
Given that \(\left| k \right| = 5 \Rightarrow k = \pm 5\)
Taking \(k = 5\), \(3\cos \alpha + 4\sin \alpha = 5\)
or \(\frac{3}{5}\cos \alpha + \frac{4}{5}\sin \alpha = 1\), this is possible only when \(\cos \alpha = \frac{3}{5}\) and \(\sin \alpha = \frac{4}{5}\)
Similarly when \(3\cos \alpha + 4\sin \alpha = 5\) or \(\frac{3}{5}\cos \alpha + \frac{4}{5}\sin \alpha = - 1\), this is possible only when \(\cos \alpha = - \frac{3}{5}\) and \(\sin \alpha = - \frac{4}{5}\).
Hence there are two possible values of \(\alpha \), so there are two solutions.

The first value of \(\theta \) satisfying the equations \(\tan \theta = \frac{1}{{\sqrt 3 }},\;\sin \theta = - \frac{1}{2}\) lies in third quadrant and the value is \(\pi + \frac{\pi }{6} = \frac{{7\pi }}{6}\). The general value of \(\theta \) can be obtained by adding a multiple of \(2\pi \).
General value = \(2n\pi + \frac{{7\pi }}{6}\)

We know that \(\cos 2\theta = \frac{{1 - {{\tan }^2}\theta }}{{1 - {{\tan }^2}\theta }}\)
Given that \(\cos 2\theta = \frac{{1 - {{\tan }^2}\theta }}{{1 - {{\tan }^2}\theta }} = \frac{1}{3} \Rightarrow {\tan ^2}\theta = \frac{1}{2}\)
Putting this value in the equation, we have,
\(32{\left( {\frac{1}{2}} \right)^4} = 2{\cos ^2}\alpha - 3\cos \alpha \)
\( \Rightarrow (2\cos \alpha + 1)(\cos \alpha - 2) = 0\)
Or \(\cos \alpha = - \frac{1}{2} \Rightarrow \alpha = 2n\pi \pm \frac{{2\pi }}{3}\)

\({\tan ^{ - 1}}\sqrt {x(x + 1)} = \frac{\pi }{2} - {\sin ^{ - 1}}\sqrt {{x^2} + x + 1} \)
\( \Rightarrow {\tan ^{ - 1}}\sqrt {x(x + 1)} = {\cos ^{ - 1}}(\sqrt {{x^2} + x + 1} )\)
Put \(x(x + 1) = y\), then
\({\tan ^{ - 1}}\sqrt y = {\cos ^{ - 1}}\sqrt {y + 1} = {\sec ^{ - 1}}\left( {\frac{1}{{\sqrt {y + 1} }}} \right)\)
Using \({\sec ^2}\theta = 1 + {\tan ^2}\theta \), we have
\(\frac{1}{{y + 1}} - 1 = y \Rightarrow y = 0,\, - 2\)
And the corresponding real values of \(x = 0,\, - 1\)

The value of \({\cos ^{ - 1}}(x)\) is \(\pi - {\cos ^{ - 1}}x\)

\({\cos ^{ - 1}}\frac{x}{2} + {\cos ^{ - 1}}\frac{y}{3} = {\cos ^{ - 1}}\left( {\frac{{xy}}{6} - \sqrt {1 - \frac{{{x^2}}}{4}} \sqrt {1 - \frac{{{y^2}}}{9}} } \right)\)
\( \Rightarrow {\cos ^{ - 1}}\left( {\frac{{xy}}{6} - \frac{{\sqrt {4 - {x^2}} \sqrt {9 - {y^2}} }}{6}} \right) = \phi \)
\( \Rightarrow xy - \sqrt {36 - 4{y^2} - 9{x^2} + {x^2}{y^2}} = 6\cos \phi \)
\( \Rightarrow {(xy - 6\cos \phi )^2} = 36 - 4{y^2} - 9{x^2} + {x^2}{y^2}\)
\( \Rightarrow 9{x^2} - 12xy\cos \phi + 4{y^2} = 36{\sin ^2}\phi \)

The given equation can be written as
\(4{\cos ^2}x + 4{\sin ^2}x + 2{\sin ^2}x = 5\)
\( \Rightarrow {\sin ^2}x = \frac{1}{2} = {\sin ^2}\frac{\pi }{4}\)
\( \Rightarrow x = n\pi \pm \frac{\pi }{4}\)

We know that \(\sin x = x\) has only one solution, that is \(x = 0\). Hence \({n_2} = 1\)
Also \(x = \,|{\sin ^{ - 1}}x|\) has one solution \(x = 0\). Hence \({n_1}-{n_2}=0\)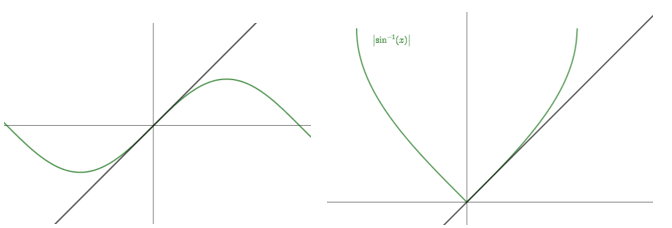

 
Intersection of \(y = x\) with \(y = \sin x\) and \(y = \,|{\sin ^{ - 1}}x|\)