Geometry can be used in solving probability questions in which variables are continuous and it is not possible to count favourable number of cases as well as total number of cases.  These questions can be converted to equivalent geometrical problems and can easily be solved using either length, area or volume depending upon the nature of question. Let us take a simple example.

If a real number is selected between 0 to 1, then what is the probability that number will be more than 0.6. 

We see here, that the number can be taken from the range 0 to 1 and the favourable range is 0.6 to 1, so the favourable range is 0.4 and the total possible interval is 1 is the probability should be 0.4

Take another example that can be solved using area. 
Suppose we are selecting a point randomly inside the given square so what is the probability that the point lies inside the shaded part where the shaded part is one fourth of the square.  intuitively the answer should be 1 by 4 and the Favourable area is one fourth of the total available area.

Probability = \(\cfrac{{{\rm{Favourable}}\;{\rm{area}}}}{{{\rm{Total}}\;\;{\rm{area}}}} = \frac{1}{4}\)

Example  01: A point is randomly selected inside a circle of radius 4 cm, find the probability that this point is closer to the centre than to circumference

Suppose there is a line that is equidistant from the centre and circumference of the circle

Required probability = \(\cfrac{{{\rm{shaded}}\;\;{\rm{area}}}}{{{\rm{total}}\;\;{\rm{area}}}}\) = \(\cfrac{1}{4}\)

Example  02:  A rod of length L is divided randomly into three parts find the probability that a triangle is formed by these three parts.

Suppose the rod is AB and there are two points P & Q such that AP = x and PQ = y, so that QB = L – x – y as we know that sum of two sides of a triangle is greater than the 3rd side.
x + y > (L – x – y) y + (L – x – y) > x (L – x – y) > y
or x + y > L/2, x < L/2, y < L/2 x > 0, y > 0, L – x – y > 0
Thus x > 0, y > 0, x + y < L (This is the sample space)  
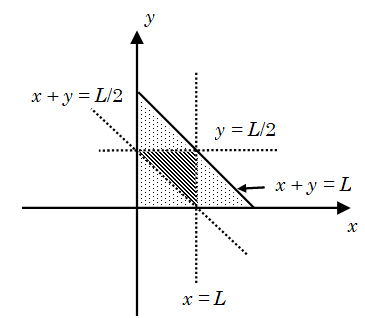
Plotting lines x + y = L, x + y = L/2, x = L/2 y = L/2.
Now favorable area is the shaded area of the middle triangle.
Required probability = \(\cfrac{1}{4}\)