CAT 2019 Quantitative Ability Slot 01
(Total questions: 34)
Question 01: In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys, pass an examination, the percentage of the girls who do not pass is:
Difference in number of girls and number of boys = 20% of the total number of students. Given that number of girls is 30 more than the number of boys, thus 20% of the total number of students = 30 or total number of students = 150.
Number of girls = 60% of 150 = 90 Number of students passed = 68% of 150 = 102 Number of boys who passed the exam = 30.
Number of girls who passed the exam = 102 – 30 = 72
Number of girls who did not pass the exam = 90 – 72 = 18.
Percentage of the girls who did not pass is \( \cfrac{18}{90}\times 100 = 20% \)
Question 02: In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
(1) 1.5
(2) 3.5
(3) 0.5
(4) 2.5
Given that CD is the diameter = 22 cm.
CE = 7, hence ED = 15 cm
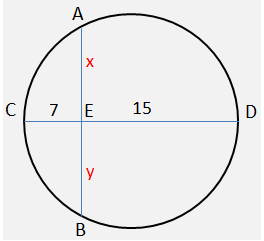
In the circle, we know that, AExEB = CExED
Thus xy = 7×15 = 105 and x + y = 20.5
Now (x – y)² = (x + y)² – 4xy = 20.5² – 4×105
or (x – y)² = 0.25
Thus difference of AE and EB = 0.5
Question 03: With rectangular axes of coordinates, the number of paths from (1,1) to (8,10) via (4,6), where each step from any point \((x,\,y)\) is either to \((x, y+1)\) or to \((x+1, y)\) is
Let us first calculate the number of paths from a point \((x_1, y_1)\) to \((x_2, y_2)\). Suppose A is (0, 0) and B is (4, 3). From A to B, there are 7 steps, 4 horizontal and 3 vertical. To reach from A to B, a total of 7 steps have to be taken, out of which 4 are horizontal and 3 are vertical steps. Among 4 horizontal steps and among 3 vertical steps order is not important. If we select any 4 horizontal steps out of total 7 steps, remaining 3 steps are automatically selected. Hence the number of ways = \(^{\rm{7}}{{\rm{C}}_{\rm{4}}}{\rm{ = }}{{\rm{ }}^{\rm{7}}}{{\rm{C}}_{\rm{3}}}\) = 35.
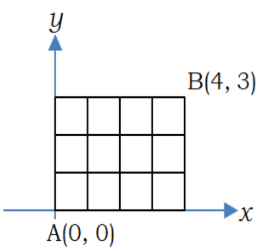
In general number of paths from the point \((x_1, y_1)\) to \((x_2, y_2)\) is \(^{({x_2} - {x_1} + {y_2} - {y_1})}{{\rm{C}}_{({x_2} - {x_1})}}\)
In this question suppose A = (1,1), B = (8,10) and C = (4,6)
Number of horizontal and vertical steps from A to C are 3 and 5, thus the number of paths from A to C = \(^{\rm{8}}{{\rm{C}}_{\rm{3}}}{\rm{ }}\) = 56.
Number of horizontal and vertical steps from C to B are 4 and 4, thus the number of paths from C to B = \(^{\rm{8}}{{\rm{C}}_{\rm{4}}}{\rm{ }}\) = 70.
Therefore number of paths from A to B via C = 56×70 = 3920
Question 04: If (5.55)x = (0.555)y = 1000, then the value of \(\cfrac{1}{x} - \cfrac{1}{y}\) is:
(a) 1
(b) 1/3
(c) 2/3
(d) 3
We know that if \({a^x} = b\), then \(a = {b^{1/x}}\), here
\({5.55^x} = 1000 \Rightarrow 5.55 = {1000^{1/x}}\)
\({0.555^y} = 1000 \Rightarrow 0.555 = {1000^{1/y}}\)
Dividing the first equation by second, we have
\(\frac{{5.55}}{{0.555}} = {1000^{\frac{1}{x} - \frac{1}{y}}}\)
\( \Rightarrow 10 = {1000^{\frac{1}{x} - \frac{1}{y}}}\)
Hence \(\cfrac{1}{x} - \cfrac{1}{y} = \frac{1}{3}\).
Question 05: A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
(1) 32
(2) 43
(3) 38
(4) 45
Suppose number of players of Football, Tennis and Cricket are represented by n(F), n(T) and n(C), then
n(F) = 144, n(T) = 123 and n(C) = 132
Also n(FnT) = 58, n(FnC) = 63 and n(TnC) = 25
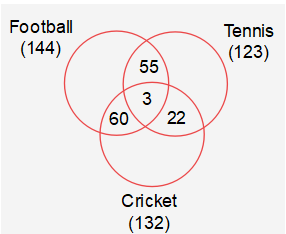
Now n(FUTUC) = n(F) + n(T) + n(C) – n(FnT) – n(FnC) – n(TnC) + n(FnTnC)
or 256 = 144 + 123 + 132 – 58 – 63 – 25 + n(FnTnC)
or n(FnTnC) = 3
Thus number of members who can play only tennis = 123 – 55 – 3 – 22 = 43
Question 06: Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
(1) 75
(2) 80
(3) 60
(4) 70
Suppose total marks in the examination = T and pass marks = x, then
40% of T + 50% of 40% of T = x – 35
=> 0.60T = x – 35 .......(1)
Again marks are increased by 20%, i.e. 0.60T + 20% of 0.60T = 0.72T
=> 0.72T = x + 7 .........(2)
From equations (1) and (2), 0.12T = 42 or T = 350.
From the equation (1), x = 0.60T + 35 = 60% of T + 35
Note that 35 is 10% of T, thus x = 60% of T + 10% of T = 70% of T
Question 07: Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is:
(1) 5 : 6
(2) 3 : 4
(3) 2 : 3
(4) 4 : 5
We know that each exterior angle of any regular hexagon = 60°. Thus \(\angle {\rm{UPA}} = \angle {\rm{PUA}} = \angle {\rm{PAU}} = {60^ \circ }\) so AP = PU = UA
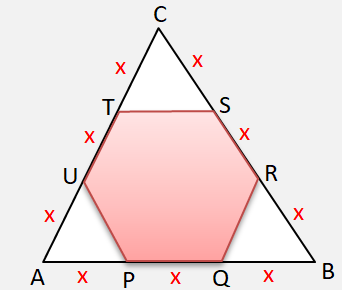
Similarly it can be shown easily that angle CTS and angle QRB are also equilateral. Area of the hexagon, H = \(6 \times \frac{{\sqrt 3 }}{4}{x^2}\)
Area of the equilateral triangle ABC, T = \(\frac{{\sqrt 3 }}{4}{(3x)^2}\)
Ratio H : T = 6 : 9 = 2: 3
Question 08: Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is:
The line 3x + 5y = 45 cuts the x axis at A (15, 0) and y axis at B(0, 9). Since the triangle AOB is a right angled, so AB is the diameter of its circum-circle.
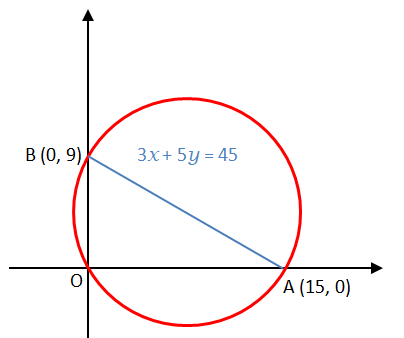
Diameter of the circle, AB = \(\sqrt{15^2+9^2}=\sqrt{306}\) we know that \(\sqrt{306}\) lies between 17 and 18, so the radius lies between 8.5 to 9. The value of radius closest to the nearest integer = 9
Question 09: For any positive integer \(n\), let \(f(n) = n(n + 1)\) if n is even, and \(f(n) = n + 3\) if \(n\) is odd. If \(m\) is a positive integer such that \(8f(m + 1) - f(m) = 2\), then \(m\) equals
There are two possible cases:
Case (i) \(m\) is even, then \(m + 1\) will be odd and
\(f(m) = m(m + 1) f(m + 1) = m + 1 + 3 = m + 4\)
Using the relation \(8f(m + 1) - f(m) = 2\), we have
\(8(m + 4) – m(m + 1) = 2\)
=> \(m^2 – 7m – 30 = 0\) or \((m – 10)(m + 3) = 0\), or \(m = 10\) as \(m\) is positive.
Case (ii) \(m\) is odd, then \(m + 1\) will be even and \(f(m) = m + 3\)\(f(m + 1) = (m + 1)(m + 2) = {m^2} + 3m + 2\).
Using the relation \(8f(m + 1) - f(m) = 2\), we have
\(8({m^2} + 3m + 2) - (m + 3) = 2\)
\( \Rightarrow 8{m^2} + 23m + 14 = 0\)
Above equation will not have positive roots as all the signs are positive. Thus value of \(m\) is unacceptable. Hence m can have only one value i.e. \(m = 10\)
Question 10: If the population of a town is p in the beginning of any year then it becomes 3+2p in the beginning of the next year. If the population in the beginning of 2019 is 1000, then the population in the beginning of 2034 will be:
(1) (1003) 15 + 6
(2) (977)15 - 3
(3) (1003)×215 - 3
(4) (977)×214 + 3
Given that initial population (in 2019) = 1000
Population after 1 year = 2×1000 + 3
Population after 2 years = 2×(2×1000 + 3) + 3 = 22×1000 + 9
Population after 3 years = 2×(22×1000 + 9) + 3 = 23×1000 + 21
It is clear that population after 15 years (in 2034) will have a factor of 215, so choice (3) can be correct. Let us write the population again in the format of the number given in the choice (3).
Population after 1 year = 2×1000 + 3 = 2×(1003 – 3) + 3 = 2×1003 – 3
Population after 2 years = 22×1000 + 9 = 22×(1003 – 3) + 9 = 22×1003 – 3
Population after 3 years = 23×1000 + 21 = 23×(1003 – 3) + 21 = 23×1003 – 3
clearly choice (3) is correct.
Question 11: A person invested a total amount of Rs 15 lakh. A part of it was invested in a fixed deposit earning 6% annual interest, and the remaining amount was invested in two other deposits in the ratio 2 : 1, earning annual interest at the rates of 4% and 3%, respectively. If the total annual interest income is Rs 76000 then the amount (in Rs lakh) invested in the fixed deposit was:
Suppose the amount invested in two other deposits = 2x and x (in lakhs), so the amount invested in fixed deposit = (15 – 3x) lakhs.
Total interest earned is (15 – 3x)×100000×0.06 + (2x)×100000×0.04 + (x)×100000×0.03 = 76000
=> 90 – 18x + 8x + 3x = 76 or x = 2 lakhs.
Hence amount invested in fixed deposit = 15 – 2x – x = 15 – 6 = 9 lakhs
Question 12: The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157 : 3, then the sum of the two numbers is:
(1) 50
(2) 85
(3) 95
(4) 58
Suppose the numbers are x and y, then
\(\cfrac{{{x^3} - {y^3}}}{{{{(x - y)}^3}}} = \cfrac{{157}}{3}\) => \(\cfrac{{(x - y)({x^2} + {y^2} + xy)}}{{{{(x - y)}^3}}} = \cfrac{{157}}{3}\)
\(\cfrac{{({x^2} + {y^2} + xy)}}{{{{(x - y)}^2}}} = \cfrac{{157}}{3}\)
Lets change the expression in the form of (x + y), we have \(\cfrac{{{{(x + y)}^2} - xy}}{{{{(x + y)}^2} - 4xy}} = \cfrac{{157}}{3}\)
Put (x + y) = k,
\( \Rightarrow \cfrac{{{k^2} - xy}}{{{k^2} - 4xy}} = \cfrac{{157}}{3}\) or \(154{k^2} = 625xy = 625 \times 616\) Thus k2 = 625×4 or k = 50.
Question 13: On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees?
(1) 80
(2) 85
(3) 100
(4) 95
On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees?
Suppose the cost price of pen is 100p and that of a book is 100b, then
– 5p + 15b = 7 and
5p + 10b = 13
Adding both the equations, we have
25b = 20 or b = 0.8
Cost price of the book = 100b = Rs. 80.
Question 14: Two cars travel the same distance starting at 10:00 am and 11:00 am, respectively, on the same day. They reach their common destination at the same point of time. If the first car travelled for at least 6 hours, then the highest possible value of the percentage by which the speed of the second car could exceed that of the first car is:
(1) 20
(2) 10
(3) 35
(4) 25
Suppose the time taken in the journey by the first and second car are (t + 1) and t.
Let the speeds of the cars are v1 and v2, and the length of the journey is d, then
\(\frac{d}{{{v_1}}} = t + 1\) and \(\frac{d}{{{v_2}}} = t\)
Dividing first equation by second, we have \(\frac{{{v_2}}}{{{v_1}}} = \frac{{t + 1}}{t} = 1 + \frac{1}{t}\)
Given that first car travelled for at least 6 hours, so t + 1 ≥ 6 or t ≥ 5.
When t is minimum, then the ratio \(\frac{{{v_2}}}{{{v_1}}}\) will be the largest, thus \(\frac{{{v_2}}}{{{v_1}}}\) = 1.20
Question 15: At their usual efficiency levels, A and B together finish a task in 12 days. If A had worked half as efficiently as she usually does, and B had worked thrice as efficiently as he usually does, the task would have been completed in 9 days. How many days would A take to finish the task if she works alone at her usual efficiency?
(1) 18
(2) 12
(3) 24
(4) 36
Suppose work done per day by A and B are a and b, then 12(a + b) = total work = W
when A works half as efficiently as she usually does, and B works thrice as efficiently as he usually does, the work done in 9 days is 9(0.5a + 3b) = total work = W
As the total wok remains the same, hence 12a + 12 b = 4.5a + 27b => a = 2b and W = 36b = 18a
Time taken by A alone to finish the work = (18a)/a = 18 days
Question 16: If \({a_1} + {a_2} + {a_3} + ..... + {a_n} = 3({2^{n + 1}} - 2)\), then the value of \({a_{11}}\)is:
11th term can also be written as: \(({a_1} + {a_2} + {a_3} + ..... + {a_{11}}) - ({a_1} + {a_2} + {a_3} + ..... + {a_{10}})\) \( = 3({2^{12}} - 2) - 3({2^{11}} - 2)\)
\( = 3({2^{12}} - {2^{11}}) = 3 \times {2^{11}}(2 - 1)\) = 6144
Question 17: The number of the real roots of the equation 2cos(x(x + 1)) = 2x + 2-x is:
(1) 0
(2) Infinite
(3) 1
(4) 2
We know that for any two positive numbers, arithmetic mean ≥ Geometric Mean
\(\frac{{{2^x} + {2^{ - x}}}}{2} \ge \sqrt {{2^x}{2^{ - x}}} \)
\( \Rightarrow {2^x} + {2^{ - x}} \ge 2\)
The value 2 is obtained at x = 0 only. But the value of 2cos (x(x + 1) will always be less than or equal to 2. So the two values will be equal at x = 0 only.
Question 18: The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala's income goes down by 4% and Bimala's goes up by 10%, then the percentage by which Kamala's income would exceed Bimala's is nearest to:
(1) 28
(2) 29
(3) 31
(4) 32
Question 19: If 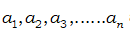 are in AP, then the value of the sum
are in AP, then the value of the sum  is
is
Question 20: In a race of three horses, the first beat the second by 11 metres and the third by 90 metres. If the second beat the third by 80 metres, what was the length, in metres, of the racecourse?
Suppose length of the racecourse is x. In the same time first, second and third horses are covering the distances x, (x – 11) and (x – 90) m. Ratio of the speeds of the second and third horses = (x – 11) : (x – 90) Also when second horse covers x metres, in the same time the third covers (x – 80) m, so ratio of their speeds = x : (x – 80)
\(\frac{{x - 11}}{{x - 90}} = \frac{x}{{x - 80}}\) \( \Rightarrow {x^2} - 91x + 880 = {x^2} - 90x\)
Hence x = 880 m
Question 21: AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to:
(1) 8.5
(2) 9.3
(3) 9.1
(4) 7.8
We know that angle subtended by diameter at any point of the circumference is 90°, so the angles P and Q are 90°.
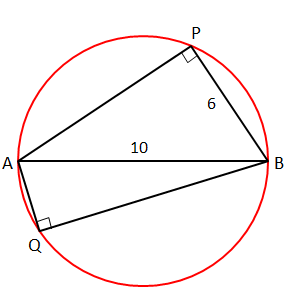
Now AP2 = 102 – BP2 = 102 – 62 = 64 or AP = 8 and AQ = 8/2 = 4
Now BQ2 = 102 – 42 = 84 or BQ = √84 = 9.16 closest answer among the 4 choices is 9.1
Question 22: One can use three different transports which move at 10, 20, and 30 kmph, respectively. To reach from A to B, Amal took each mode of transport 1/3 of his total journey time, while Bimal took each mode of transport 1/3 of the total distance. The percentage by which Bimal's travel time exceeds Amal's travel time is nearest to:
(1) 22
(2) 19
(3) 21
(4) 20
Suppose total time taken by Amal is 3t, and as Amal took each mode of transport 1/3 of his total journey time, so the total journey is 10t + 20t + 30t = 60t
As Bimal took each mode of transport 1/3 of the total distance, total time taken by Bimal = (20t/10) + (20t/20) + (20t/30) = 3t + (2t/3)
Required percentage = \(\frac{{3t + \frac{{2t}}{3} - 3t}}{{3t}} \times 100 = 22.22\% \)
Choice (1) is the correct answer.
Question 23: Amala, Bina, and Gouri invest money in the ratio 3 : 4 : 5 in fixed deposits having respective annual interest rates in the ratio 6 : 5 : 4. What is their total interest income (in Rs) after a year, if Bina's interest income exceeds Amala's by Rs 250?
(1) 7000
(2) 6000
(3) 6350
(4) 7250
Interest earned is directly proportional to rate of interest × amount invested Thus ratio of the interest earned = (3×6) : (4×5) : (5×4) = 18 : 20 : 20
Suppose their interest incomes are 18x, 20x and 20x
Difference in the income Bina and Amla = 20x – 18x = 2x = 250
=> x = 125
So the total income = 18x + 20x + 20x = 58x = 58×125 = 7250.
Question 24: If m and n are integers such that \({\left( {\sqrt 2 } \right)^{19}}{3^4}{4^2}{9^m}{8^n} = {3^n}{16^m}\left( {\sqrt[4]{{64}}} \right)\) then m is
(1) –16
(2) – 24
(3) – 12
(4) – 20
Arranging powers of 2 and 3, we have
\({2^{\frac{{19}}{2}}} \cdot {3^4} \cdot {2^4} \cdot {3^{2m}} \cdot {2^{3n}} = {3^n} \cdot {2^{4m}} \cdot {2^{\frac{6}{4}}}\)
\( \Rightarrow {2^{\frac{{19}}{2} + 4 + 3n}} \cdot {3^{2m + 4}} = {3^n} \cdot {2^{\frac{6}{4} + 4m}}\)
Equating powers of 2 and 3, we have, \(n = 4 + 2m\) \(4m = 12 + 3n\)
Solving the above equations, m = – 12
Question 25: A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is:
(1) 70
(2) 85
(3) 80
(4) 75
Weight of liquid 1 per litre = 1000 g
Weight of liquid 2 per litre = 800 g
Weight of the mixture 1 per litre = 2×480 = 960 g
Using Alligation rule,
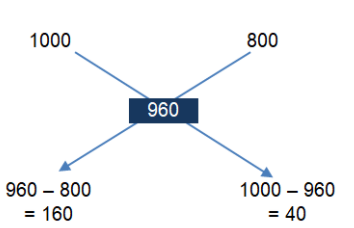
The ratio of liquid 1 and liquid 2 in the mixture = 4 : 1, so the liquid 1 is 80% of the mixture.
Question 26: Let x and y be positive real numbers such that log5(x + y) + log5(x – y) = 3, and log2y – log2x = 1 – log23, then xy equals:
(1) 25
(2) 150
(3) 250
(4) 100
The first equaltion log5(x + y) + log5(x – y) = 3 can be written as log 5(x + y)(x – y) = 3
=> x2 – y2 = 53 = 125 ............(1)
and the second equation can be written as log 2y – log2x = log22 – log23
=> log2(y/x) = log2(2/3) or y/x = 2/3
Let x = 3k and y = 2k, from equation (1), 9k 2 – 4k2 = 125 or k2 = 25
Now xy = (3k)(2k) = 6k2 = 150
Question 27: If the rectangular faces of a brick have their diagonals in the ratio 3 : 2√3 : √15, then the ratio of the length of the shortest edge of the brick to that of its longest edge is:
(1) 1 : √3
(2) 2 : √5
(3) √2 : √3
(4) √3 : 2
Suppose the lengths of the three diagonals are 3k, 2√3k and √15k, and the three sides are a, b and c, then a 2 + b2 = 9k2
b2 +c2 = 12k2
c2 + a2 = 15k2
Adding the three equations, 2(a2 + b2 + c2 ) = 36k2
=> a2 + b2 + c2 = 18k2
Thus a2 = 6k2, b2 = 3k2 and c2 = 9k2
Ratio of the shortest and the longest sides = 1 : √3
Question 28: Let S be the set of all points (x,y) in the x-y plane such that |x| + |y| ≤ 2 and |x| ≥ 1. Then, the area, in square units, of the region represented by S equals
|x| + |y| = 2 represents 4 lines, x + y = 1, x – y = 1, – x – y = 1 and – x + y = 1. These four lines represent a square. |x| = 1 represents two straight lines x = 1 and x = – 1. The line x = 1 cuts the graph |x| +|y| = 2 at two points (1, 1) and (1, – 1), similarly the line x = –1 cuts the graph |x| +|y| = 2 at two points (–1, 1) and (–1, – 1) The region S is shown by the shaded part.
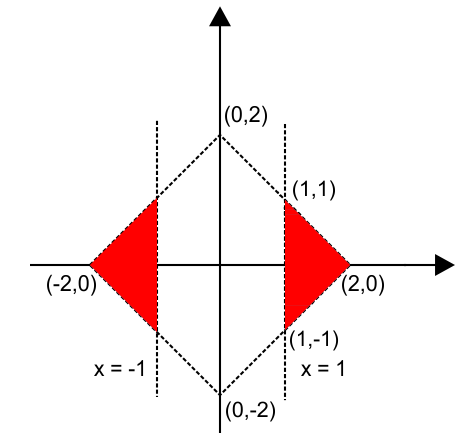
Area of the shaded part = 2×area of triangle
Area of one triangle = (1/2)×base×height = (1/2)×2×1 = 1
Area of the region S = 2
Question 29: The number of solutions of the equation |x|(6x2 + 1) = 5x2 is
We know that |x| = x, when x > 0 and |x| = – x, when x < 0 x = 0 is a clear solution of the equation.
case 1: x > 0, |x| = x(6x2 + 1) = 5x2 => 6x2 + 1 = 5x or (3x – 1)(2x – 1) = 0. Thus x = 1/3 and x = 1/2
case 2: x < 0, |x| = – x(6x2 + 1) = 5x2 => 6x2 + 1 = – 5x or (3x + 1)(2x + 1) = 0. Thus x = – 1/3 and x = – 1/2 Hence there are 5 solutions.
Question 30: Three men and eight machines can finish a job in half the time taken by three machines and eight men to finish the same job. If two machines can finish the job in 13 days, then how many men can finish the job in 13 days?
Suppose one day work of a machine and a man are represented by M and m, then one day work by 3 men and 8 machines is double of 3 machines and 8 men (3m + 8M) = 2(3M + 8m)
=> M = (13/2) m
Work done by a machine in one day is 13/2 times that of a man.
Thus 2 machine can do the same work as 13 men do.
Question 31: The product of the distinct roots of |x2 – x – 6| = x + 2 is:
(1) – 4
(2) – 16
(3) – 8
(4) – 24
The expression |x2 – x – 6| = |(x + 2)(x – 3)|
When x ≥ 3 or x ≤ – 2, |(x + 2)(x – 3)| = (x + 2)(x – 3)
So the equation |x2 – x – 6| = x + 2 can be written as (x + 2)(x – 3) = (x + 2) => (x + 2)(x – 4) = 0
=> x = – 2 or x = 4
Both the solutions are in acceptable range.
When –2 ≤ x ≤ 3, |(x + 2)(x – 3)| = – (x + 2)(x – 3)
So the equation |x2 – x – 6| = x + 2 can be written as – (x + 2)(x – 3) = (x + 2)
=> – (x + 2)(x – 2) = 0 => x = – 2 or x = 2
Both the solutions are in acceptable range.
Hence product of the roots = – 2×2×4 = – 16
Question 32: The wheels of bicycles A and B have radii 30 cm and 40 cm, respectively. While traveling a certain distance, each wheel of A required 5000 more revolutions than each wheel of B. If bicycle B traveled this distance in 45 minutes, then its speed, in km per hour, was
(1) 18π
(2) 16π
(3) 12π
(4) 14π
Suppose each wheel of B requires n revolutions and each wheel of A requires n + 5000 revolutions, then 2π(0.4)×n = 2π(0.3)×(n + 5000)
=> n = 15000 Total distance = 2π(0.4)×15000 m = 12π km
This is covered in 45 m = 0.75 hours
Speed of B = \(\frac{{12\pi }}{{0.75}} = 16\pi \)
Question 33: : Consider a function \(f(x+y) = f(x) f(y)\) where x , y are positive integers, and f(1) = 2. If f (a+1) + f (a+2) + ..... + f(a+n) = 16 (2n - 1) then a is equal to:
Given that f(1) = 2, thus f(2) = f(1 + 1) = f(1)f(1) = 22
f(3) = f(1 + 2) = f(1)f(2) = 2×22 = 23
f(4) = f(1 + 3) = f(1)f(3) = 2×23 = 24
So we can generalize as \(f(n) = 2n\)
Now we can calculate: f (a+1) = f(a)f(1) = 2f(a)
f (a+2) = f(a)f(2) = 22f(a)
f (a+3) = f(a)f(2) = 23f(a) and so on.
The sum f (a+1) + f (a+2) + ..... + f(a+n) will be
2f(a) + 22f(a) + 23f(a) + ......+2n f(a) = \(\frac{{2f(a)[{2^n} - 1]}}{{(2 - 1)}} = 2f(a)[{2^n} - 1]\)
But the sum is given as 16 (2n – 1) Hence 2f(a) = 16 or f(a) = 8 or a = 3.
Question 34: Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is
(1) 51
(2) 53
(3) 49
(4) 48
Given that The average score of all the 22 students is 1 more than the average score of the 21 students other than Ramesh, it means average score increases by 1 when Ramesh is included. So score of Ramesh should be 22×1 more than the average of other 21.
Average of other 21 = 82.5 – 22 = 60.5
Average of all 22 is 60.5 + 1 = 61.5
The average score of the 21 students other than Gautam is 62, that mean average score decreases by 0.5 when Gautam is included, score of Gautam should be 22×0.5 less than the average of other 21 = 62 – 22×0.5 = 51.
Alternate Method: Suppose score of Gautam is g and total score of 20 students other that Gautam and Ramesh is x, then 82.5 + x = 21×62 Solving these equations, g = 51.