Example 4: Rahul takes 25 days to finish a job alone, while Avinash takes 10 days to finish the same job. What is the ratio of their efficiency?

Solution: Rahul needs 25 days and Avinash needs 10 days to do the work then ratio of time taken by Rahul and Avinash is 5 : 2. The efficiency will be in the ratio 2 : 5 as efficiency is inversely proportional to the time taken. Thus Avinash is 2.5 times faster than Rahul. 

Example 5: If Damru is thrice as efficient as Kamru and is therefore able to finish piece of work in 48 days less than Kamru, find the time in which Damru and Kamru can complete can complete the work working together? 

Solution: Suppose Damru takes x days to complete the work, then Kamru will take 3x days to complete the same work. Given that

\(3x-x = {\rm{ }}48 \Rightarrow x = {\rm{ }}24\) and \(3x = 72\). 

Thus, Damru needs 24 days while Kamru needs 72 days to complete the work independently.

Thus one day’s work of Damru and kamru will be: \(\frac{1}{{24}} + \frac{1}{{72}} = \frac{1}{{18}}\). Thus total time required to complete the work together will be 18 days.

Example 6: It takes 6 technicians a total of 10 hours to build a new server from direct Computer, with each working at the same rate. If six technicians start to build the server at 11:00 AM, and one technician per hour is added beginning at 5:00 PM, at what time will the server be complete? 

Solution: Total time taken to build the server = 60 man hours. 6 of them start at 11:00 AM and work till 5 PM. They will complete \(6 \times 6{\rm{ }} = {\rm{ }}36\) man hours of work. At 5 PM they will have 24 more man hours of work to complete. 

Between 5 PM and 6 PM they will complete 7 man hours.

Between 6 PM and 7 PM they will complete 8 man hours.

Between 7 PM and 8 PM they will complete 9 man hours.

So, totally they will complete 36 + 7 + 8 + 9 = 60 man hours by 8PM. 

Example 7: \(A, B\) and \(C\) can complete a work working alone in 10, 20 and 60 days respectively. \(A\) started the work and after 2 days and \(B\) & \(C\) also joined him. Find the total time required to complete the work.

Solution:  The following diagram indicates the workings of \(A, B\) and \(C\). 

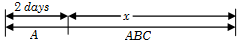
Work done by \(A\) in the first 2 days \( = \,\,\,\frac{2}{{10}} = \frac{1}{5}\)

Remaining work (i.e. 4/5) is completed by \(A, B\) and \(C\) together.

Hence \(x = \frac{{4/5}}{{\frac{1}{{10}} + \frac{1}{{20}} + \frac{1}{{20}}}} = \frac{{48}}{{6 + 3 + 1}} = 4.8\,\,\,days\)

Hence total time occupied = \(2 + 4.8 = 6.8\) days 

Example 8: \(A\) and \(B\) working together can complete a work in \(\frac{{20}}{3}\)days, while \(B\) and \(C\) can complete in \(\frac{{60}}{7}\) days and \(A\) and \(C\) can do the work in \(\frac{{15}}{2}\) days. What is number of days required for \(A, B\) and \(C\) to complete the work independently.

Solution: Work done by \(A\) and \(B\) in 1 day = \(\frac{3}{{20}}\)

Work done by \(B\) and \(C\) in 1 day = \(\frac{7}{{60}}\)

Work done by \(C\) and \(A\) in 1 day = \(\frac{2}{{15}}\)

Thus, work done by \(A, B\) and \(C\) together in 1 day 

\(\frac{1}{2}\left( {\frac{3}{{20}} + \frac{7}{{60}} + \frac{2}{{15}}} \right) = \frac{1}{2}\left( {\frac{{9 + 7 + 8}}{{60}}} \right) = \frac{1}{5}\)

Thus, work done by \(C\) in one day = \(\frac{1}{5} - \frac{3}{{20}} = \frac{1}{{20}}\)

\(B\) in one day = \(\frac{1}{5} - \frac{2}{{15}} = \frac{1}{{15}}\)

\(A\) in one day = \(\frac{1}{5} - \frac{7}{{60}} = \frac{1}{{12}}\)

Thus, the number of days required by \(A, B\) and \(C\) independently are 12, 15 and 20 respectively. 

2. By taking LCM

Let the work be LCM of \(\frac{{20}}{3},\frac{{60}}{7},\frac{{15}}{2} = \frac{{60}}{1}\)units

Contribution of \(A\) and \(B\) = \(\frac{{60}}{{20/3}} = 60 \times \frac{3}{{20}} = 9\)

Contribution of \(B\) and \(C = \frac{{60}}{{60/7}} = 60 \times \frac{7}{{60}} = 7\)

Contribution of \(A\) and \(C = \frac{{60}}{{15/2}} = 60 \times \frac{2}{{15}} = 8\)

Contribution of \(A, B\) and \(C = \frac{{9 + 7 + 8}}{2} = 12\)

Contribution of \(A\) in one day 

= Contribution by \((A + B + C)\) - contribution by 

\((B + C) = 12 - 7 = 5\) 

Thus, number of days required days by A to complete the work is 

= \(\frac{{Number\,of\,units}}{{Contribution\;of\;\,A}} = \frac{{60}}{5} = 12\)

Similarly, we can find the required number of days for \(B\) and \(C\).

Example 9: \(A\) is twice as efficient as \(B\) and they complete a work in 12 days. Find the times required by each to complete the work individually.

Solution: When we say A is twice as efficient as \(B\). it means that \(A\) will take half the time taken by \(B\) to complete the work individually suppose \(B\) takes \(2x\) days to complete the work alone then \(A\) will take \(x\) days to complete the same work alone.

Hence \(\frac{1}{x} + \frac{1}{{2x}} = \frac{1}{{12}}\)  

\(\therefore \frac{3}{{2x}} = \frac{1}{{12}} \Rightarrow x = \frac{{12 \times 3}}{2} = 18\)

Hence \(A\) and \(B\) will take 18 and 36 days respectively to complete the work working alone  

Example 10: \(A, B, C\) can complete a certain project working alone in 10, 15 and 20 days respectively. They worked on this project together for 2 days, then \(A\) left. \(B\) left the project one day earlier than the completion of the project. Find the total time to complete the project.

Solution: The following diagram shows the working of \(A, B\) and \(C\).

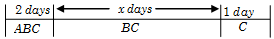
We see that \(C\) has worked for \((x + 3)\) days, \(A\) has worked for 2 days and \(B\) has worked for \((x + 2)\) days. 

Hence \((x + 3)\left[ {\frac{1}{{20}}} \right] + (2 + x)\left[ {\frac{1}{{15}}} \right] + \frac{2}{{10}} = 1\)

or \(7x = {\rm{ }}31 \Rightarrow \) \(x =\frac{{31}}{7}\)

Total time taken =\(2 + 1 + \frac{{31}}{7}\) =\(\frac{{52}}{7}\) days

Example 11: 30 men can do a work in 10 days working together. All men started the work together but after 3 days, 10 men left. Find total time required to complete the work 

Solution: Total work  =  \(30 \times 10{\rm{ }} = {\rm{ }}300\) man days. 

Total work done in first 3 days 

\( = {\rm{ }}3 \times 30{\rm{ }} = {\rm{ }}90\) man days   

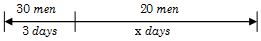
Remaining work = 300 - 90 = 210

Time required  \( = \frac{{210}}{{20}} = 10.5\) days 

Hence total time required = 3 + 10.5 = 13.5 days