(a) When  distance is constant,  time is inversely proportional to speed, which means if speed is  doubled, time taken will be halved, if speed becomes one third, time taken becomes tripled etc. the following example explains the concept in details.

If a student increases his speed by \(33\frac{1}{3}\% \), he reaches his school 20 min early. Find the usual time taken by the student to reach the school.

When a man drives his car 25% faster than his usual speed he reaches his office 30 minutes earlier than the usual time. At what percent of the usual speed should he drive so that he reaches his office 20 minutes late than the usual time? 

(b) When the time is constant, then the distance covered is directly proportional to the time taken. This concept is generally used in cases when two or more objects start moving together and they meet after a certain time.

\(A, B\) start moving from a point P towards \(Q\). Ratio of the speed of \(A\) & \(B\) is 7:3 \(A\) after reaching \(Q\), returns towards \(P\). Find the point where they meet. Given that  \(PQ = 200\) m.

This is the case where time is constant. So the ratio of distances covered by \(A\) & \(B\) and in the ratio of their speeds.

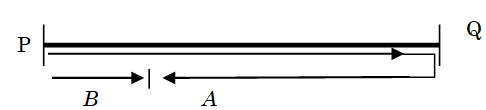
By the diagram, we see that total distance covered by \(A\) & \(B\) together is 400 m. Ratio of distances covered by \(A\) & \(B\) is 7:3
B covered  \(3 \times \) \(\frac{1}{{10}}\) \( \times 400\) = 120
So they meet at a point i.e. 120 m away from \(P\).

Example 5: A man coves a certain distance on scooter. Had he moved 3 km/hr faster, he would have taken 20 min less. If he had moved 2 km/hr slower, he would have taken 20 min more. Find the original speed. 

Solution: Suppose the original speed is \(v\) and the original time taken is \(t\) min, then \[\frac{{(v + 3)(t - 20)}}{{60}} = \frac{{vt}}{{60}} = \frac{{(v - 2)(t + 20)}}{{60}}\]

From the above relations,

\( \Rightarrow 3t-{\rm{ }}20v = {\rm{ }}60\) and

\(- 2t + 20v = 40\) 

Solving these equations we have,

\(t  = 100\) min and \(v = 12\) km/hr

Also the distance = \(12 \times \frac{{100}}{{60}} = 20km\)

Note: A man covers a certain distance \(D\). If he moves \(‘u’\) kmph faster, he would have taken \(T\) time less and if he moves \(‘v’\) kmph slower, he would have taken \(T\) time more. The original speed is given by  \(\cfrac{{2uv}}{{u - v}}\)

Example 6: A boy walking at a speed of 10 km/h reaches his school 12 min late. Next time at a speed of 15 km/h reaches his school 7 min late. Find the distance of his school from his house?

Solution: Increase in the speed is 50%, it means that the speed becomes \(\frac{3}{2}\) times, thus the time taken must be \(\frac{2}{3}\) times of the initial time and one third of the time is saved. Initial time is 12 min late and now the time taken is 7 min late.  Difference between the time = \(12 - 7 = 5\) min

Thus one third of the time is 5 min, or the initial time must be 15 min and the initial speed us 10 km/hr. Thus total distance = \(10 \times \frac{{15}}{{60}} = 2.5\) km.

Example 7: A train after moving 70 kms meets with an accident and it speed becomes 3/4th of the original hence it reaches the destination 36 minutes late. Had the accident been at 85 kms from the starting point the train would have been late only by 24 minutes late. Find the speed of the train. 

Solution: Suppose usual speed of the train is v and the distance \(PQ =  x\)

Method I:

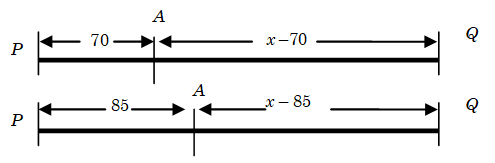
According to the first condition:

\(\frac{{70}}{v} + \frac{{x - 70}}{{\frac{3}{4}v}} = \frac{x}{v} + \frac{{36}}{{60}}\) (1)

\(\frac{{85}}{v} + \frac{{x - 85}}{{\frac{3}{4}v}} = \frac{x}{v} + \frac{{24}}{{60}}\) (2)

Subtracting equation (2) from (1), we get

\(-\frac{{15}}{v} + \frac{{15}}{{\frac{3}{4}v}} = \frac{{12}}{{60}}\) \( \Rightarrow \) v = 25 kms/hour.

Method II:  we observe that the difference in the time is because of the middle 15 kms. In the first case train is running at normal speed and in the second case it is running at 3/4th of the normal speed. 

\(\frac{{15}}{{(\frac{3}{4}v)}} - \frac{{15}}{v} = \frac{{12}}{{60}}\)

Hence \(v = 25\) km/hr

Example 8:  If A travels at 50 kmph he reaches his college 14 minutes late and if he increases his speed to 60 kmph he reaches 16 minutes too soon. Find the distance he is traveling.

Solution:  \(\frac{x}{{50}} - \frac{x}{{60}} = \frac{{16 + 14}}{{60}}\)

\(\frac{x}{{300}} = \frac{1}{2}\)\( \Rightarrow x\) = 150 km.