Past Papers Solutions: CAT 2021 Quantitative Ability

CAT 2021 Quantitative Ability - Slot 02

2021 QA Slot 02

CAT 2021 Quantitative Ability Slot 02
(Total questions : 22)

Question 01: The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is

1000

This question is based on the concepts that the number of solutions of the equation \({x_1} + {x_2} + {x_3} + ..... + {x_r} = n\), where each variable is a non-negative integer is \(^{n + r - 1}{{\rm{C}}_{r - 1}}\)

Number of ways of distributing identical balloons is same as the number of solution of the equation \(x + y + z = 15\), where \(x,\,y,\,z\) are integers and more than or equal to 4. Let us first give 4 balloons to each and the remaining 3 are redistributed among them.

Number of ways = \(^{3 + 3 - 1}{{\rm{C}}_{3 - 1}} = \,{\,^5}{{\rm{C}}_2} = 10\)

Similarly 6 identical pencils can be distributed among them such that each one is getting a least one pencil in \(^{3 + 3 - 1}{{\rm{C}}_{3 - 1}} = 10\)

Also 3 identical erasers can be distributed in \(^{3 + 3 - 1}{{\rm{C}}_{3 - 1}} = 10\)ways.

Total number of ways = 10×10×10 = 1000

Question 02: Consider the pair of equations: x² – xy – x = 22 and y² – xy + y = 34. If x > y, then x – y equals
(1) 8

(1) 8
(2) 6
(3) 7
(4) 4

Adding both the equations, we have

x² + y² – 2xy – (x – y) = 56

or (x – y)² – (x – y) = 56

or (x – y)(x – y – 1) = 56

As x > y, hence x – y is positive. Since 56 is easily factorized as 8×7, so (x – y) = 8

Click on Answer or Solution

Question 03: If \({\rm{lo}}{{\rm{g}}_{\rm{2}}}\left[ {{\rm{3 + lo}}{{\rm{g}}_{\rm{3}}}{\rm{\{ 4 + lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right){\rm{\} }}} \right] - {\rm{2 = 0}}\) then \(4x\) equals

Given that \({\rm{lo}}{{\rm{g}}_{\rm{2}}}\left[ {{\rm{3 + lo}}{{\rm{g}}_{\rm{3}}}{\rm{\{ 4 + lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right){\rm{\} }}} \right]{\rm{ }} = {\rm{ 2}}\)

\( \Rightarrow {\rm{3 + lo}}{{\rm{g}}_{\rm{3}}}{\rm{\{ 4 + lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right){\rm{\} }} = {\rm{4}}\)

\( \Rightarrow {\rm{lo}}{{\rm{g}}_{\rm{3}}}{\rm{\{ 4 + lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right){\rm{\} }} = {\rm{1}}\)

\(\Rightarrow {\rm{4 + lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right) = 3\)

\(\Rightarrow {\rm{lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right) = - 1\) or \(x - 1 = \frac{1}{4} \Rightarrow 4x = 5\)

Click on Answer or Solution

Question 04: From a container filled with milk, 9 litres of milk are drawn and replaced with water. Next, from the same container, 9 litres are drawn and again replaced with water. If the volumes of milk and water in the container are now in the ratio of 16 : 9, then the capacity of the container, in litres, is

Suppose capacity of the container is \(x\), then fraction of the milk after replacement of 9 litres of milk with water = \(\left( {\frac{{x - 9}}{x}} \right)\).

This process is repeated again, so the fraction is = \(\left( {\frac{{x - 9}}{x}} \right)\left( {\frac{{x - 9}}{x}} \right)\)

Given that \(\left( {\frac{{x - 9}}{x}} \right)\left( {\frac{{x - 9}}{x}} \right) = \frac{{16}}{{16 + 9}}\)

\( \Rightarrow \frac{{x - 9}}{x} = \frac{4}{5}\) or \(x = 45\)

Read more about repeated replacement ►

Click on Answer or Solution

Question 05: Two trains A and B were moving in opposite directions, their speeds being in the ratio 5 : 3. The front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other. It took another 69 seconds for the rear ends of the trains to cross each other. The ratio of length of train A to that of train B is

(1) 2 : 3
(2) 2 : 1
(3) 5 : 3
(4) 3 : 2

2 : 3

Suppose lengths of the trains A and B are \({\ell _a}\) and \({\ell _b}\), their speeds are \(5k\) and \(3k\). As it is given that the front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other, hence

\(\frac{{{\ell _b}}}{{5k + 3k}} = 46\)

Also it took another 69 seconds for the rear ends of the trains to cross each other, so

\(\frac{{{\ell _a}}}{{5k + 3k}} = 69\)

Dividing the equations, we have \(\frac{{{\ell _b}}}{{{\ell _a}}} = \frac{{46}}{{69}} = \frac{2}{3}\)

Click on Answer or Solution

Question 06: Anil can paint a house in 60 days while Bimal can paint it in 84 days. Anil starts painting and after 10 days, Bimal and Charu join him. Together, they complete the painting in 14 more days. If they are paid a total of ₹ 21000 for the job, then the share of Charu, in INR, proportionate to the work done by him, is

(1) 9000
(2) 9100
(3) 9200
(4) 9150

9100

Let the total work is LCM (60, 84) = 420 units.

One day’s work of Anil and Bimal are 7 and 5. Suppose one day’s work of Charu is c, then

10×7 + 14×(7 + 5 + c) = 420

\( \Rightarrow \) c = 13.

Ratio of the quantities of the work done by them = 24×7 : 14×5 : 14×13 = 12 : 5 : 13

Share of Charu \( = \frac{{13}}{{12 + 5 + 13}} \times 21000 = 9100\)

Click on Answer or Solution

Question 07: A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is

250

Suppose metallic white balls = metallic black balls = n. So n = 40% of white balls = 50% of black balls.

Hence number of white balls = 2.5n and number of black balls = 2n.

Total balls = 450, therefore 2.5n + 2n = 450 or n = 100

Number of metallic balls = 2n = 200

Number of nonmetallic balls = 450 – 200 = 250.

Click on Answer or Solution

Question 08: Anil, Bobby and Chintu jointly invest in a business and agree to share the overall profit in proportion to their investments. Anil's share of investment is 70%. His share of profit decreases by ₹ 420 if the overall profit goes down from 18% to 15%. Chintu's share of profit increases by ₹ 80 if the overall profit goes up from 15% to 17%. The amount, in INR, invested by Bobby is:
(1)

(1) 2400
(2) 2200
(3) 2000
(4) 1800

2000

Anil's share is 70%. Suppose total investment is a, then 3% change in profit means a change in Anil’s share, that is 0.03×0.70a.

Given that 0.03×0.70a = 420 or a = 20000

Chintu’s profit goes up by ₹ 80, when overall profit goes up by 2%.
So (0.02a)×Chintu's share = 80

Hence Chintu’s share = \(\frac{{80}}{{0.02 \times 20000}} \times 100 = 20\% \)

Bobby’s share = 100 – 70 – 20 = 10%

Bobb’s investment is also 10% = 0.10×20000 = 2000

Click on Answer or Solution

Question 09: If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is

(1) √37 + 13√2
(2) √13 + 12√2
(3) √(37) + √(13)
(4) √(13) + √(12)

√(37) + √(13)

The height of the rhombus is ED, then area = 5×ED = 12 or \({\rm{ED}} = \frac{{12}}{5}\)

\( \Rightarrow E{A^2} = A{D^2} - D{E^2} = {5^2} - {\left( {\frac{{12}}{5}} \right)^2} = \frac{{481}}{{25}}\)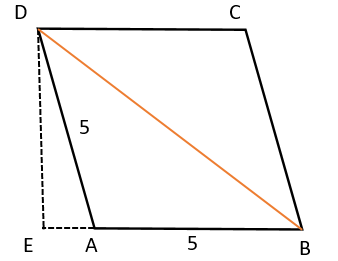

Now the bigger diagonal,

\(B{D^2} = {(AB + AE)^2} + D{E^2}\)

\( = {\left( {5 + \frac{{\sqrt {481} }}{5}} \right)^2} + {\left( {\frac{{12}}{5}} \right)^2} = 50 + 2\sqrt {481} \)

\( \Rightarrow BD = \sqrt {50 + 2\sqrt {481} } = \sqrt {37 + 13 + 2\sqrt {37 \times 13} } \)

\( = \sqrt {37} + \sqrt {13} \)

Click on Answer or Solution

Question 10: Three positive integers x, y and z are in arithmetic progression. If y − x > 2 and xyz = 5(x + y + z), then z − x equals

(1) 8
(2) 10
(3) 14
(4) 12

Given that, x, y and z are in Arithmetic Progression, so 2y = x + z

Also given that xyz = 5(x + y + z).

xyz = 5(3y)

or xz = 15

Since y - x > 2, hence z – x > 4.

and possible values of x and z are (1, 15).

So, x = 1, y = 8, z = 15

Click on Answer or Solution

Question 11: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is

Area of the triangle ADE = \(\frac{1}{2}(2k)(2x)\sin A\)

Area of the triangle ABC = \(\frac{1}{2}(3k)(5x)\sin A\)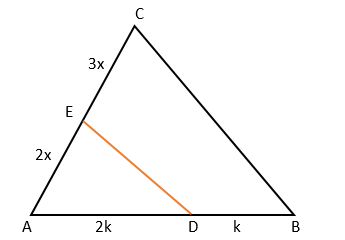

\( \Rightarrow \frac{{{\rm{Area}}\;{\rm{of}}\;{\rm{ADE}}}}{{{\rm{Area}}\;{\rm{of}}\;{\rm{ABC}}}} = \frac{4}{{15}}\)

Hence Area of ABC = 30.

Click on Answer or Solution

Question 12: For a 4-digit number, the sum of its digits in the thousands, hundreds and tens places is 14, the sum of its digits in the hundreds, tens and unit’s places is 15, and the tens place digit is 4 more than the unit’s place digit. Then the highest possible 4-digit number satisfying the above conditions is:

4195

Suppose the number is abcd, then

a + b + c = 14 and b + c + d = 15

\( \Rightarrow \)a = d – 1

In order to maximize the number, a has to be maximum, for that d has to be maximum. Also b = 4 + d, so the maximum value of d can be 5.

Therefore, d = 5, a = 4 and b = 9.

The number is 4195

Click on Answer or Solution

Question 13: For all values of \(x\), the range of the function \(f(x) = \frac{{{x^2} + 2x + 4}}{{2{x^2} + 4x + 9}}\) is:

(1) \(\left[ {\frac{3}{7},\;\,\frac{8}{9}} \right]\)
(2) \(\left[ {\frac{4}{9},\;\,\frac{8}{9}} \right]\)
(3) \(\left[ {\frac{3}{7},\;\left. {\frac{1}{2}} \right)} \right.\)
(4) \(\left( {\frac{3}{7},\;\frac{1}{2}} \right)\)

\(\left[ {\frac{3}{7},\;\left. {\frac{1}{2}} \right)} \right.\)

The expression can be written as \(\cfrac{1}{2}\left[ {\frac{{2{x^2} + 4x + 8}}{{2{x^2} + 4x + 9}}} \right] = \frac{1}{2}\left[ {1 - \frac{1}{{2{x^2} + 4x + 9}}} \right]\)

We know that minimum value of \(a{x^2} + bx + c = \frac{{4ac - {b^2}}}{{4a}}\), when \(a > 0\).

Here minimum value of \(2{x^2} + 4x + 9 = \frac{{4 \times 2 \times 9 - 16}}{{4 \times 2}} = 7\) and maximum value of \(2{x^2} + 4x + 9\) is infinite. Though the infinite is obtained when \(x\) is also infinite. So we can only say that the value of \(2{x^2} + 4x + 9\) approaches to infinity.

Putting these values we get two corresponding values of \(f(x)\) as \(\frac{3}{7}\)and \(\frac{1}{2}\). Note that the value exact \(\frac{1}{2}\) is not obtained. So \(\frac{3}{7} \le f(x) < \frac{1}{2}\)

Click on Answer or Solution

Question 14: In a football tournament, a player has played a certain number of matches and 10 more matches are to be played. If he scores a total of one goal over the next 10 matches, his overall average will be 0.15 goals per match. On the other hand, if he scores a total of two goals over the next 10 matches, his overall average will be 0.2 goals per match. The number of matches he has played is:

Let the number of matches already played be n.

Given that over the next ten matches if one more goal is scored, the average goals become 0.15.

Also if the player scores two goals the average becomes 0.2.

From this we can see that one extra goal is increasing the average of \(n + 10\) matches by 0.05

\( \Rightarrow \frac{1}{{n + 10}} = 0.05\) or \(n = 10\)

Click on Answer or Solution

Question 15: For all possible integers \(n\) satisfying \(2.25 \le 2 + {2^{n + 2}} \le 202\), the number of integer values of \(3 + {3^{n + 1}}\) is

The given inequality can be written as \(0.25 \le {2^{n + 2}} \le 200\)

We know that \(0.25 = \frac{1}{4}\) and \({2^8} = 256\)

\( \Rightarrow - 2 \le n + 2 \le 7\) or \( - 4 \le n \le 5\)

Now we have to find integer values of \(3 + {3^{n + 1}}\), so \(n + 1 \ge 0\) or \(n \ge - 1\)

Therefore \(n\) can take the following values \( - 1,\,\,0,\,\,1,\,\,2,\;3,\;4,\;5\).

Click on Answer or Solution

Question 16: For all real numbers \(x\) the condition \(|3x - 20| + |3x - 40|\, = 20\) necessarily holds if

(1) \(6 < x < 11\)
(2) \(7 < x < 12\)
(3) \(10 < x < 15\)
(4) \(9 < x < 14\)

\(7 < x < 12\)

Let \(y = \,\,|3x - 20| + |3x - 40|\)

We see that value of \(y\) is always positive, let us find the value of \(y\) at \(x = \frac{{20}}{3}\) and \(x = \frac{{40}}{3}\).

The values of \(y\) at these points are same and equal to 20.

If we take values of \(x\) greater than \(\frac{{40}}{3}\) or smaller than \(\frac{{20}}{3}\), then \(y\) will increase and will have a value more than 20.

Hence \(\frac{{20}}{3} \le x \le \frac{{40}}{3}\)

Only choice (2) gives the most appropriate range.

Click on Answer or Solution

Question 17: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

(1) 20
(2) 25
(3) 40
(4) 30

AB and CD are parallel sides and P is the midpoint, so areas of the ▲DPA, ▲APB and ▲PBC are equal, suppose it is x.

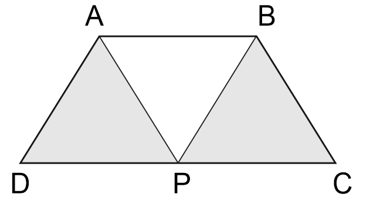
Areas of the parallelogram ABPD – area of triangle BPC = 10

\( \Rightarrow \)2x – x = 10 or x = 10

Area of the trapezium = 3x = 30

Click on Answer or Solution

Question 18: Raj invested ₹ 10000 in a fund. At the end of first year, he incurred a loss but his balance was more than ₹ 5000. This balance, when invested for another year, grew and the percentage of growth in the second year was five times the percentage of loss in the first year. If the gain of Raj from the initial investment over the two year period is 35%, then the percentage of loss in the first year is

(1) 15
(2) 5
(3) 10
(4) 70

Given that his balance was more than ₹ 5000 at the end of the first year, so the percentage loss in the first year is less than 50.

Suppose the percentage loss was \(r\% \) and in two years his gain was 35%, so

\(\left( {1 - \frac{r}{{100}}} \right)\left( {1 + \frac{{5r}}{{100}}} \right) = 1.35\)

Suppose \(\frac{r}{{100}} = x\)

\( \Rightarrow (1 - x)(1 + 5x) = 1.35\)

It can be solved by putting values of \(x\) from the choices. (\(x\)should be less than 0.50)

Solving the quadratic equation,

\(1 + 4x - 5{x^2} = 1.35\)

\( \Rightarrow 100{x^2} - 80x + 7 = 0\)

\( \Rightarrow (10x - 7)(10x - 1) = 0\)or \(x\)= 0.10, 0.70.

Hence \(r = 10\% \)

Click on Answer or Solution

Question 19: Suppose one of the roots of the equation \(a{x^2} - bx + c = 0\) is \(2 + \sqrt 3 \) where \(a\), \(b\) and \(c\) are rational numbers and \(a \ne 0\). If \(b = {c^3}\) then \(|a|\) equals

(1) 2
(2) 3
(3) 4
(4) 1

Given that \(a\), \(b\) and \(c\) are rational numbers, if one roots is \(2 + \sqrt 3 \), other will be \(2 - \sqrt 3 \).

Sum of the roots = \(\frac{b}{a} = 4\) or \(b = 4a\)

Product of the roots = \(\frac{c}{a} = 1\) or c = a

As \(b = {c^3}\), so \(4a = {a^3}\) or \({a^2} = 4\) or \(|a| = 2\)

Click on Answer or Solution

Question 20: For a sequence of real numbers \({x_1},{x_2},...,{x_n}\), if \({x_1} - {x_2} + {x_3} - ..... + {( - 1)^{(n + 1)}}{x_n} = {n^2} + 2n\) for all natural numbers \(n\), then the sum \({x_4}_9 + {x_5}_0\) equals
(1) (1) 2
(2) – 2
(3) 200
(4) – 200

– 2

Putting \(n = 48,\;49,\;50\) we get the following values,

\({x_1} - {x_2} + {x_3} - ...... + {x_{47}} - {x_{48}} = {48^2} + 2 \times 48 = 2400\)

\({x_1} - {x_2} + {x_3} - ...... + {x_{47}} - {x_{48}} + {x_{49}} = {49^2} + 2 \times 49 = 2499\)

\({x_1} - {x_2} + {x_3} - ...... - {x_{48}} + {x_{49}} - {x_{50}} = {50^2} + 2 \times 50 = 2600\)

Subtract first equation from the second equation,

\({x_{49}} = 99\)

Subtract third equation from the second equation,

\({x_{50}} = - 101\)

\( \Rightarrow {x_{49}} + {x_{50}} = - 2\)

Click on Answer or Solution

Question 21: Two pipes A and B are attached to an empty water tank. Pipe A fills the tank while pipe B drains it. If pipe A is opened at 2 pm and pipe B is opened at 3 pm, then the tank becomes full at 10 pm. Instead, if pipe A is opened at 2 pm and pipe B is opened at 4 pm, then the tank becomes full at 6 pm. If pipe B is not opened at all, then the time, in minutes, taken to fill the tank is

(1) 140
(2) 120
(3) 144
(4) 264

144

Suppose pipe A fills a litres per hours and pipe B empties b litres per hours, the

8a – 7b = 4a – 2b = C, where C is the capacity of the tank.

\( \Rightarrow \)a : b = 5 : 4

Take a = 5 litres per hours and b = 4 litres per hours, then C = 12 litres and A alone can fill it is \(\frac{{12}}{5}\;{\rm{hr}}\) or \(\frac{{12}}{5} \times 60 = 144\) minutes.

Click on Answer or Solution

Question 22: A person buys tea of three different qualities at ₹ 800, ₹ 500, and ₹ 300 per kg, respectively, and the amounts bought are in the proportion 2 : 3 : 5. She mixes all the tea and sells one-sixth of the mixture at ₹ 700 per kg. The price, in INR per kg, at which she should sell the remaining tea, to make an overall profit of 50%, is

(1) 692
(2) 688
(3) 653
(4) 675

688

The mean price of the tea = \(\frac{{2 \times 800 + 3 \times 500 + 5 \times 300}}{{2 + 3 + 5}} = 460\)

In order to have a profit of 50%, the mean selling price should be 1.50×460 = ₹ 690/kg. Given that she sells one-sixth of the mixture at ₹ 700 per kg, let the selling price of the reaming five –sixth is \(x\), then

\(\frac{1}{6} \times 700 + \frac{5}{6}x = 690\)

\( \Rightarrow x = 688\)

Click on Answer or Solution

CAT 2021 Quantitative Ability - Slot 02

Question 01: The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is

Question 02: Consider the pair of equations: x² – xy – x = 22 and y² – xy + y = 34. If x > y, then x – y equals(1) 8

Question 03: If \({\rm{lo}}{{\rm{g}}_{\rm{2}}}\left[ {{\rm{3 + lo}}{{\rm{g}}_{\rm{3}}}{\rm{\{ 4 + lo}}{{\rm{g}}_{\rm{4}}}\left( {x - 1} \right){\rm{\} }}} \right] - {\rm{2 = 0}}\) then \(4x\) equals

Question 07: A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is

Question 09: If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is

Question 10: Three positive integers x, y and z are in arithmetic progression. If y − x > 2 and xyz = 5(x + y + z), then z − x equals

Question 11: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is

Question 13: For all values of \(x\), the range of the function \(f(x) = \frac{{{x^2} + 2x + 4}}{{2{x^2} + 4x + 9}}\) is:

Question 15: For all possible integers \(n\) satisfying \(2.25 \le 2 + {2^{n + 2}} \le 202\), the number of integer values of \(3 + {3^{n + 1}}\) is

Question 16: For all real numbers \(x\) the condition \(|3x - 20| + |3x - 40|\, = 20\) necessarily holds if

Question 17: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

Question 19: Suppose one of the roots of the equation \(a{x^2} - bx + c = 0\) is \(2 + \sqrt 3 \) where \(a\), \(b\) and \(c\) are rational numbers and \(a \ne 0\). If \(b = {c^3}\) then \(|a|\) equals

Question 02: Consider the pair of equations: x² – xy – x = 22 and y² – xy + y = 34. If x > y, then x – y equals
(1) 8