Question 01: In a car race, car A beats car B by 45 km, car B beats car C by 50 km, and car A beats car C by 90 km. The distance (in km) over which the race has been conducted is
(1) 550
(2) 475
(3) 500
(4) 450
450
Let the length of the race track be \(x\) km and speed of A, B and are \(a,\;b,\;c\), then
By the time A finishes the race, B lags by 45 km.
Ratio of Speeds of A and B,
\(\frac{a}{b} = \frac{x}{{x - 45}}\) …. (1)
By the time B finishes the race, C lags by 50 km.
Ratio of Speeds of B and C,
\(\frac{b}{c} = \frac{x}{{x - 50}}\) ……(2)
By the time A finishes the race, C lags by 90 km.
Ratio of Speeds of A and C,
\(\frac{a}{c} = \frac{x}{{x - 90}}\)…….(3)
We see that the ratio \(\frac{a}{c}\)can be obtained by multiplying equation (1) and equation (2),
\(\left( {\frac{x}{{x - 45}}} \right)\,\left( {\frac{x}{{x - 50}}} \right) = \frac{x}{{x - 90}}\)
\( \Rightarrow {x^2} - 90x = {x^2} - 95x + 2250\)
Therefore \(x = 450\)
..
Click on Answer or Solution
Question 02: From the interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the perpendiculars is s. Then the area of the triangle is
(1) \(\frac{{{s^2}}}{{2\sqrt 3 }}\)
(2) \(\frac{{2{s^2}}}{{\sqrt 3 }}\)
(3) \(\frac{{{s^2}}}{{\sqrt 3 }}\)
(4) \(\frac{{\sqrt 3 {s^2}}}{2}\)
\(\frac{{{s^2}}}{{\sqrt 3 }}\)
Suppose side of the triangle is \(a\), then sum of areas of the triangles APB, BPC and CPA is equal to the area of the triangle ABC. In the given triangle PX, PY and PZ are the perpendiculars. Given that PX + PY + PZ = s

\( \Rightarrow \frac{{a\left( {PX} \right)}}{2} + \frac{{a\left( {PY} \right)}}{2} + \frac{{a\left( {PZ} \right)}}{2} = \frac{{\sqrt 3 }}{4}{a^2}\)
\( \Rightarrow (PX + PY + PZ) = \frac{{\sqrt 3 a}}{2}\)
\( \Rightarrow a = \frac{{2s}}{{\sqrt 3 }}\) and area of the triangle ABC = \(\frac{{\sqrt 3 }}{4}{\left( {\frac{{2s}}{{\sqrt 3 }}} \right)^2} = \frac{{{s^2}}}{{\sqrt 3 }}\)
..
Click on Answer or Solution
Question 03: In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
(1) 5
(2) 3
(3) 4
(4) 6
4
Shortcut: The question is asking about two extreme values of the average, so we should consider the two extreme values of the scores. Since the average of the first 9 scores is 42, we can assume all the first 9 numbers two be
42 and the tenth number is x,
x + 8×42 = 9×47 or x = 87
Case 2: Since the average of the last 9 scores is 47, we can assume all the last 9 numbers two be 47, and the first number is y, then
y + 8×47 = 9×42 or y = 2
Thus minimum sum of the 10 scores = 2 + 9×47 = 425 and maximum sum of the 10 scores =9×42 + 87 = 465
The difference = 465 – 425 = 40. Hence the difference between the maximum and minimum average = 40/10 = 4
Detailed Method: Suppose the scores are \({a_1} < {a_2} < {a_3} < ...... < {a_9} < {a_{10}}\), where \({a_1},\;{a_{10}}\) are the smallest and highest scores. Given that
\({a_1} + {a_2} + {a_3} + ...... + {a_9} = 9 \times 42 = 378\)
\({a_2} + {a_3} + ...... + {a_9} + {a_{10}} = 9 \times 47 = 423\)
From these two equations, \({a_{10}} - {a_1} = 423 - 378 = 45\)
Adding the two equations, we have
\({a_1} + 2({a_2} + {a_3} + {a_4} + ... + {a_9}) + {a_{10}} = 801\)
\( \Rightarrow 2({a_1} + {a_2} + {a_3} + {a_4} + ... + {a_9} + {a_{10}}) = 801 + {a_1} + {a_{10}}\)
Average of all the scores = \(\frac{{{a_1} + {a_2} + {a_3} + ....{a_{10}}}}{{10}} = \frac{{801 + {a_1} + {a_{10}}}}{{20}}\)
Now we have to find minimum and maximum values of \({a_1} + {a_{10}}\), that will minimize and maximize the overall average of all the scores.
Since average of the first 9 scores is 42, so \({a_1} \le 42\) and \({a_{10}} = 45 + 42 = 87\), so the average of all the scores will be \(\frac{{801 + 129}}{{20}} = \frac{{930}}{{20}} = 46.4\)
Since average of the last 9 scores is 47, so \({a_{10}} \ge 47\) and \({a_1} = 47 - 45 = 2\), so the average of all the scores will be \(\frac{{801 + 49}}{{20}} = \frac{{850}}{{20}} = 42.5\)
Difference = 46.5 – 42.5 = 4.
..
Click on Answer or Solution
Question 04: The number of pairs of integers(x, y) satisfying x ≥ y ≥ -20 and 2x + 5y = 99 is:
17
The first solution by observation is x = 2 and y = 19. Now in the solutions, x will increase at the rate of 5 and y will decrease at the rate of 2. So the general values of x and y can be written as
x = 5n + 2 and y = 19 – 2n. By putting any integer value of n, we get the corresponding values of x and y, and that will be a solution of 2x + 5y = 99.
Since x ≥ y ≥ – 20, so
5n + 2 ≥ 19 – 2n or n ≥ 3
Also 19 – 2n ≥ – 20 or n ≤ 19
Therefore 3≤ n ≤ 19, so there are 17 solutions
..
Click on Answer or Solution
Question 05: The value of \({\log _a}\frac{a}{b} + {\log _b}\frac{b}{a}\), for \(1 < a \le b\) cannot be equal to
(1) – 0.5
(2) 1
(3) 0
(4) – 1
1
\({\log _a}\frac{a}{b} + {\log _b}\frac{b}{a} = {\log _a}a - {\log _a}b + {\log _b}b - {\log _b}a\)
\( = 2 - {\log _a}b - {\log _b}a = 2 - \left( {{{\log }_a}b + \frac{1}{{{{\log }_b}a}}} \right)\)
We know that \(x + \frac{1}{x} \ge 2\) or \(x + \frac{1}{x} \le - 2\)
Hence \(2 - \left( {{{\log }_a}b + \frac{1}{{{{\log }_b}a}}} \right) \le 0\;\;{\rm{or}}\;\; \ge 4\), it cannot be equal to 1 in any case.
..
Click on Answer or Solution
Question 06: Let the mth and nth terms of a Geometric progression be \(\frac{3}{4}\) and 12, respectively, when m < n. If the common ratio of the progression is an integer r, then the smallest possible value of r + n – m is
(1) – 4
(2) – 2
(3) 6
(4) 2
– 2
Given that,
\({T_m} = a{r^{m - 1}} = \frac{3}{4}\)
\({T_n} = a{r^{n - 1}} = 12\)
\(\frac{{a{r^{n - 1}}}}{{a{r^{m - 1}}}} = \frac{{12}}{{\,\,(3/4)\,\,}} = 16\)
\( \Rightarrow {r^{n - m}} = 16\), there are two possibilities; \({( \pm 2)^4} = 16\;\;{\rm{or}}\;\;{( \pm 4)^2} = 16\)
Hence for minimum value of \(r + n - m\), we should take \(r = - 4,\,\,n - m = 2\)
..
Click on Answer or Solution
Question 07: If \(x\) and \(y\) are positive real numbers satisfying \(x + y = 102\), then the minimum possible value of \(2601\left( {1 + \frac{1}{x}} \right)\left( {1 + \frac{1}{y}} \right)\) is
2704
\(2601\left( {1 + \frac{1}{x}} \right)\left( {1 + \frac{1}{y}} \right) = 2601\left( {1 + \frac{{x + y + 1}}{{xy}}} \right)\)
The expression is minimum when \(xy\) is maximum.
We know that when \(x + y\) is given, then \(xy\) is maximum when \(x = y\). Here \(xy\)is maximum when \(x = y = 51\).
Hence minimum value of the expression is:
\(2601\left( {1 + \frac{1}{{51}}} \right)\left( {1 + \frac{1}{{51}}} \right) = 2704\)
..
Click on Answer or Solution
Question 08: For the same principal amount, the compound interest for two years at 5% per annum exceeds the simple interest for three years at 3% per annum by Rs 1125. Then the principal amount in rupees is:
90000
Let the principal be p, then
compound interest for two years at 5% = p(1.05)² – p = 0.1025p
simple interest for three years at 3% = 0.03×3p = 0.09p
Given that 0.1025p – 0.09p = 1125 or p = 90000
..
Click on Answer or Solution
Question 09: Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to:
(1) 6.6
(2) 7.2
(3) 8.8
(4) 7.8
8.8
OAB is a right angled triangle, so AB = 5, suppose OM is perpendicular to AB, then
\(\frac{{AM \times OM}}{2} = \frac{{3 \times 4}}{2} \Rightarrow OM = 2.4\)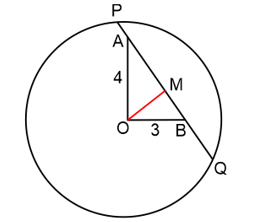
Now \(P{M^2} = O{P^2} - O{M^2} = {5^2} - {2.4^2} = 19.24\)
Length \(PQ = 2PM = 2\sqrt {19.24} \approx 8.8\)
..
Click on Answer or Solution
Question 10: For real \(x\), the maximum possible value of \(\frac{x}{{\sqrt {1 + {x^4}} }}\) is:
(1) 1
(2) \(\frac{1}{2}\)
(3) \(\frac{1}{{\sqrt 2 }}\)
(4) \(\frac{1}{{\sqrt 3 }}\)
\(\frac{1}{{\sqrt 2 }}\)
The expression can be written as \(\frac{1}{{\sqrt {{x^2} + \frac{1}{{{x^2}}}} }}\), we know that \({x^2} + \frac{1}{{{x^2}}} \ge 2\), thus minimum value of the expression is \(\frac{1}{{\sqrt 2 }}\)
..
Click on Answer or Solution
Question 11: Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
(1) 60
(2) 50
(3) 55
(4) 54
50
Suppose the labelled selling price is p, then
8×0.8p + 4×0.8×0.75p = 2112
\( \Rightarrow \)8.8p = 2112 or p = 240
Actual selling price after discount per toy = \(\frac{{2112}}{{12}} = 176\)
Since he is gaining 10% profit, so the cost price = \(\frac{{176}}{{1.1}} = 160\)
Profit without any discount = \(\frac{{240 - 160}}{{160}} \times 100 = 50\% \)
..
Click on Answer or Solution
Question 12: If x and y are non-negative integers such that x + 9 = z, y + 1 = z and x + y < z + 5, then the maximum possible value of 2x + y equals:
23
Equating the value of z from the first two equations,
x + 9 = y + 1 or y = x + 8
Now given that x + y < z + 5
\( \Rightarrow \) x + (x + 8) < (x + 9) + 5
Or x < 6 and y < 14
To maximize 2x + y, put x = 5 and y = 13, and the maximum value is 23
..
Click on Answer or Solution
Question 13: Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
(1) 22
(2) 19
(3) 20
(4) 21
20
Given that a + b + 18 = 23 and a + 18 + c = 25
Adding both the equations, we have 2a + 36 + b + c = 48
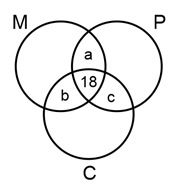
To minimize (b + c), a has to be maximum. The maximum value of a can be 5 as a + b + 18 = 23. Hence minimum value of b + c = 2, and minimum number of students who could choose chemistry as one of their subjects is 18 + 2 = 20
..
Click on Answer or Solution
Question 14: Let f(x) = x² + ax + b and g(x) = f(x + 1) – f(x – 1). If f(x) ≥ 0 for all real x, and g(20) = 72, then the smallest possible value of b is:
(1)
16
(2) 1
(3) 4
(4) 0
4
Given that, f(x+1) = f(x+1)² + a(x + 1) + b
and f(x–1) = f(x–1)² + a(x – 1) + b
\( \Rightarrow \) g(x) = (x+1)² + a(x+1) + b – (x–1)² – a(x–1) – b
= 4x + 2a
g(20) = 4(20) + 2a = 72 (given)
\( \Rightarrow \)a = – 4
Since f(x) ≥ 0, so x² – 4x + b ≥ 0
(x – 2)² + b – 4 ≥ 0 or b – 4 ≥ 0
Value of b is at least 4
..
Click on Answer or Solution
Question 15: The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is
(1) 7:5
(2) 4:1
(3) 1:4
(4) 5:7
5:7
Suppose AB = \(x\) and BC = \(3x\). Speed of train 1 for the distance AB = \(v\), then
Time taken by train 1 to travel from A to C is
\(\frac{{AB}}{v} + \frac{{BC}}{{2v}} = \frac{x}{v} + \frac{{3x}}{{2v}} = \frac{{5x}}{{2v}}\)
Time taken by train 2 to travel from A to C is
\(\frac{{AB}}{{2v}} + \frac{{BC}}{v} = \frac{x}{{2v}} + \frac{{3x}}{v} = \frac{{7x}}{{2v}}\)
The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is \(\frac{{5x/2v}}{{7x/2v}} = \frac{5}{7}\)
..
Click on Answer or Solution
Question 16: The sum of perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfy the relationship R = T². If the sides of the rectangle are in the ratio 1 : 3, then the length, in cm, of the longer side of the rectangle, is:
(1) 27
(2) 18
(3) 21
(4) 24
27
Suppose the sides of the rectangle are x and 3x, then its perimeter is 2(x + 3x) = 8x.
Let side of the equilateral triangle is \(a\), then its area = \(\frac{{\sqrt 3 }}{4}{a^2}\)
Given that \(3{x^2} = {\left( {\frac{{\sqrt 3 }}{4}{a^2}} \right)^2}\) or \(x = \frac{{{a^2}}}{4}\)
Given that the sum of perimeters of an equilateral triangle and a rectangle is 90 cm, so
\(8x + 3a = 90\)
\( \Rightarrow 2{a^2} + 3a = 90\) or \((2a + 15)(a - 6) = 0\) or \(a = 6\) and x = 9
..
Click on Answer or Solution
Question 17: The number of integers that satisfy the equality \({({x^2} - 5x + 7)^{x + 1}} = 1\) is:
(1) 5
(2) 4
(3) 3
(4) 2
3
There are 3 possibilities that lead to \({m^n} = 1\).
Case 1: \(m = 1\) and \(n\)can be any number. So \({x^2} - 5x + 7 = 1 \Rightarrow x = 2,\,\,3\)
Case 2: \(m = - 1\) and \(n\)is an even number. So \({x^2} - 5x + 7 = - 1\), but this equation has no real solution.
Case 3: \(n = 0\) and \(m\)is any non-zero number. So \((x + 1) = 0 \Rightarrow x = - 1\)
Therefore, there are 3 solutions to the given equation.
..
Click on Answer or Solution
Question 18: In how many ways can a pair of integers \((x,\;a)\) be chosen such that \({x^2} - 2|x| + |a - 2| = 0\) ?(1) 7
(2) 6
(3) 4
(4) 5
7
Let us assume that \(|a - 2|\, = k\), then the equation \({x^2} - 2|x| + k = 0\) will have real roots if \(4 - 4k \ge 0\) or \(k \le 1\). So \(k\) can take two values 0 or 1.
Case 1: \(k = 0\) or \(a = 2\) and \({x^2} - 2|x|\,\, = 0\)or \(x = 0,\; \pm 2\). Possible pairs of \((a,\,x)\)= 3.
Case 2: \(k = 1\) or \(a = 1,\,\,\,3\) and \({x^2} - 2|x|\, + 1 = 0\)or \(x = \; \pm 1\). Possible pairs of \((a,\,x)\)= 4.
Total possible pairs = 7
..
Click on Answer or Solution
Question 19: Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is:
(1) 5
(2) 3
(3) 4
(4) 2
3
We do not need to calculate the exact value of the time taken by Ram and Rahim. We can just calculate the ratio of the time taken by them to complete one round.
Ratio = \(\frac{{2\pi (100)}}{{15}}:\frac{{2\pi (20)}}{5} = 5:3\)
Suppose Ram takes 5 units and Rahim takes 3 units, then they will meet again after LCM (5, 3) = 15 units. During this time Ram have completed \(\frac{{15}}{5} = 3\) rounds.
..
Click on Answer or Solution
Question 20: A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other, Ram and Rahim reach their destinations in one minutes and four minutes, respectively. If they start at the same time, then the ratio of Ram's speed to Rahim's speed is:
(1) 2
(2) 2√2
(3) √2
(4) 3
2
This is a direct formula based question,
\(\frac{{{\rm{Speed}}\;\;{\rm{of}}\;{\rm{Ram}}}}{{{\rm{Speed}}\;\;{\rm{of}}\;{\rm{Rahim}}}}{\rm{ = }}\sqrt {\frac{{{\rm{Time}}\;{\rm{taken}}\;{\rm{by}}\;{\rm{Rahim}}}}{{{\rm{Time}}\;{\rm{taken}}\;{\rm{by}}\;{\rm{Ram}}}}} \)
\( \Rightarrow \frac{{{\rm{Speed}}\;\;{\rm{of}}\;{\rm{Ram}}}}{{{\rm{Speed}}\;\;{\rm{of}}\;{\rm{Rahim}}}}{\rm{ = }}\sqrt {\frac{{\rm{4}}}{{\rm{1}}}} = 2\)
..
Click on Answer or Solution
Question 21: Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm of C1 is
10
The chord is bisected at the point M, hence MN = 3.
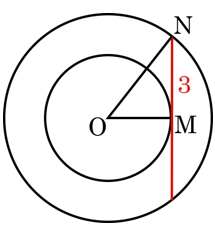
Also radius of the bigger circle is 1 more than that of the smaller circle, let us assume ON =
\(r + 1\) and OM =
\(r\).
\( \Rightarrow {(r + 1)^2} = {r^2} + {3^2}\) or \(r = 4\)
Radius of the bigger circle = 5 and diameter = 10.
..
Click on Answer or Solution
Question 22: John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?
4
Suppose one day’s work of John = x units, then one day’s work by Jack = 2x units
If one day’s work of Jim = y units, then
(2x + y) = 3x or y = x
Work per day when all three work together = 4x units.
Now (4x)n = x(n + 3) or n = 1.
Total work = 4x, so time taken by Jim = 4 days
..
Click on Answer or Solution
Question 23: In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent 450 on rice in April, then how much did he spend on wheat in May?
(1) 590
(2) 580
(3) 560
(4) 570
560
Given that John bought the same amount of rice and the same amount of wheat in both the months.
Extra expenses on rice in may = 0.20×450 = 90, hence extra expenses on wheat in may = 150 – 90 = 60. This amount 60 is because of 12% rise in the price, so the amount spent on wheat in April = \(\frac{{60}}{{0.12}} = 500\).
Amount spent on wheat in May = 500 + 60 = 560.
..
Click on Answer or Solution
Question 24: Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
(1) 33
(2) 27
(3) 30
(4) 36
33
Suppose cost of one pencil = p and that of sharpener is p + 2. Suppose Aron purchases x pencil and y sharpeners, then
xp + y(p + 2) = 2xp + (y – 10)(p + 2)
xp = 10(p + 2)
Or x = 10 + (20/p)
Now x will be minimum when p = 20, hence x = 11 and total number of pencils purchased by them = 3x = 33.
..
Click on Answer or Solution
Question 25: A sum of money is split among Amal, Sunil and Mita so that the ratio of the shares of Amal and Sunil is 3:2, while the ratio of the shares of Sunil and Mita is 4:5. If the difference between the largest and the smallest of these three shares is Rs 400, then Sunil’s share, in rupees, is
800
Ratio of the amount with Amal, Sunil and Mita = 6 : 4 : 5
Difference between the largest and the smallest of these shares is Rs 400.
6x – 4x = 400 or x = 200
Share of Sunil = Rs 800.
..
Click on Answer or Solution
Question 26: How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
315
There are 2 cases:
Case 1: In the four digits other than 7 and 3, one digit is 0, then the fourth digit can be selected in 7 ways and these four digits can be arranged such that 0 does not come at the first place in \(7 \times \left( {3 \times 3 \times 2 \times 1} \right) = 126\)
Case 2: In the four digits other than 7 and 3, both the digits are non-zero. These two digits can be selected in \(^{\rm{7}}{{\rm{C}}_{\rm{2}}} = 21\) ways. These four digits can be arranged in \(21 \times 4!\)ways.
There will be exactly same numbers in which 7 comes before 3 or 3 comes before 7.
Now numbers in which 7 comes before 3 = \(\frac{1}{2}\left( {126 + 21 \times 4!} \right)\)
= 315
..
Click on Answer or Solution



