We know that
\(\tan \theta = \cfrac{{2\sqrt {{h^2} - ab} }}{{a + b}} = \frac{{2\sqrt {\frac{{49}}{4} - 12} }}{{1 + 12}} = \frac{1}{{13}}\)
Now \(\cfrac{{2\cos \theta + 3\sin \theta }}{{4\sin \theta + 5\cos \theta }}\)= \(\frac{{2 + 3\tan \theta }}{{4\tan \theta + 5}}\)
= \(\cfrac{{2 + 3 \times \frac{1}{{13}}}}{{4 \times \frac{1}{{13}} + 5}} = \frac{{29}}{{69}}\)

\(f'(x) = \cfrac{{1(1 + x\tan x) - x(x{{\sec }^2}x + \tan x)}}{{{{(1 + x\tan x)}^2}}}\)
\( = \cfrac{{1 - {x^2}{{\sec }^2}x}}{{{{(1 + x\tan x)}^2}}}\)
Here we see that when \({x^2}{\sec ^2}x < 1,\;\;f'(x) > 0\) and when \({x^2}{\sec ^2}x > 1,\;\;f'(x) < 0\). Hence the function is maximum at \(x\sec x = 1\).
\( \Rightarrow \cos x = x\)

The numbers are \(^n{{\rm{C}}_2}\;{\rm{and}}{\;^n}{{\rm{C}}_4}\), clearly \(n \ge 4\). From the options \(n\) = 5 gives the correct ratio.

Each question can be attempted or not attempted. So there are two choices for each question. So total number of ways of attempting the paper is \({2^{50}}\), but there will be a case when no question is attempted. Except this case all other cases are to be counted. Hence the number of ways = \({2^{50}} - 1\).

Probability that none of them will die is \({(1 - p)^n}\). Hence probability that at least one of them will die is \(1 - {(1 - p)^n}\).
Now if we consider order, probability that \({A_1}\) is the first to die among \(n\)people is:
\(\frac{1}{n}\left( {1 - {{(1 - p)}^n}} \right)\)

The mean will be \(\cfrac{{\sum {fx} }}{{\sum f }} = \cfrac{{\sum\limits_{n = 0}^{50} {n{ \cdot ^{50}}{{\rm{C}}_n}} }}{{\sum\limits_{n = 0}^{50} {^{50}{{\rm{C}}_n}} }} = \cfrac{{\sum\limits_{n = 0}^{50} {n{ \cdot ^{50}}{{\rm{C}}_n}} }}{{{2^{50}}}}\) ……(1)
We know that \({(1 + x)^{50}} = {\,^{50}}{{\rm{C}}_0} + {\,^{50}}{{\rm{C}}_1}x + {\,^{50}}{{\rm{C}}_2}{x^2} + ....... + {\,^{50}}{{\rm{C}}_n}{x^n}\)
Differentiating w.r.t \(x\), we have
\(50{(1 + x)^{49}} = \,{\,^{50}}{{\rm{C}}_1} + \,2 \times {\,^{50}}{{\rm{C}}_2}x + ....... + \,50 \times {\,^{50}}{{\rm{C}}_{50}}{x^{49}}\)
Now put \(x = 1\) in the above equation,
\(50 \times {2^{49}} = \,{\,^{50}}{{\rm{C}}_1} + \,2 \times {\,^{50}}{{\rm{C}}_2} + ....... + \,50 \times {\,^{50}}{{\rm{C}}_{50}}\)
Put this value in equation (1),
Mean = \(\frac{{50 \times {2^{49}}}}{{{2^{50}}}} = 25\)
The question can be solved taking smaller values, take total numbers as 5, and you will find the mean as 2.5. From the choices we can conclude that the answer is 50/2 = 25.

We can put values of the angles A, B and C to get an idea about the value of \(k\), put A = B = C = 60°,
\(k = {\tan ^2}30 + {\tan ^2}30 + {\tan ^2}30 = 1\)
Put another set of values A = B = 30° and C = 120°,
\(k = {\tan ^2}15 + {\tan ^2}15 + {\tan ^2}45 > 1\)
Hence \(k \ge 1\)

The maximum and minimum value of \(a\cos \alpha + b\sin \alpha = \pm \sqrt {{a^2} + {b^2}} \)
Hence maximum and minimum value of \(3\cos \alpha + 4\sin \alpha = \pm 5\)
Given that \(\left| k \right| = 5 \Rightarrow k = \pm 5\)
Taking \(k = 5\), \(3\cos \alpha + 4\sin \alpha = 5\)
or \(\frac{3}{5}\cos \alpha + \frac{4}{5}\sin \alpha = 1\), this is possible only when \(\cos \alpha = \frac{3}{5}\) and \(\sin \alpha = \frac{4}{5}\)
Similarly when \(3\cos \alpha + 4\sin \alpha = 5\) or \(\frac{3}{5}\cos \alpha + \frac{4}{5}\sin \alpha = - 1\), this is possible only when \(\cos \alpha = - \frac{3}{5}\) and \(\sin \alpha = - \frac{4}{5}\).
Hence there are two possible values of \(\alpha \), so there are two solutions.

Using the half angle formula,
\(a.\left( {\frac{{s(s - c)}}{{ab}}} \right) + c.\left( {\frac{{s(s - a)}}{{bc}}} \right) = \frac{{3b}}{2}\)
\( \Rightarrow s(s - c) + s(s - a) = \frac{{3{b^2}}}{2}\)
\( \Rightarrow s(2s - a - c) = \frac{{3{b^2}}}{2}\)
Or \(\frac{{b(a + b + c)}}{2} = \frac{{3b}}{2} \Rightarrow a + c = 2b\)
The sides are in AP.

Any vector that is coplanar with \(\vec a\)and \(\vec c\) is, \(\vec a + \lambda \vec c = (2 + \lambda )\hat i + (1 + \lambda )\hat j + (2 - 2\lambda )\hat k\)
Projection on \(\vec b\)is: \((\vec a + \lambda \vec c).\hat b\) = \(\frac{{(2 + \lambda ) - (1 + \lambda ) + 2(2 - 2\lambda )}}{{\sqrt {{1^2} + {{( - 1)}^2} + {2^2}} }} = \frac{{5 - 4\lambda }}{{\sqrt 6 }}\)
Given that projection on \(\overrightarrow b \)is of magnitude \(\frac{1}{{\sqrt 6 }}\), hence \(5 - 4\lambda = 1 \Rightarrow \lambda = 1\)
The vector is: \(\vec a + \lambda \vec c = (2 + \lambda )\hat i + (1 + \lambda )\hat j + (2 - 2\lambda )\hat k\) = \(3\widehat i + 2\widehat j\)

Standard deviation does not change when we increase or decrease each number by a constant, hence it will remain 30.

Square and add both the equations,
\({a^2}({\sin ^2}\theta + {\cos ^2}\theta ) + {b^2}({\sin ^2}\theta + {\cos ^2}\theta ) = {2^2} + {3^2}\)
\( \Rightarrow {a^2} + {b^2} = 13\)

Given that, \(\log (1 - x + {x^2}) = {a_1}x + {a_2}{x^2} + {a_3}{x^3} + ..... + {a_n}{x^n}\)
Put \(x = 1,\,\,\omega ,\,\,{\omega ^2}\) respectively,
\(\log (1) = {a_1} + {a_2} + {a_3} + ..... + {a_n}\)
\(\log (1 - \omega + {\omega ^2}) = {a_1}\omega + {a_2}{\omega ^2} + {a_3}{\omega ^3} + ..... + {a_n}{\omega ^n}\)
\(\log (1 - {\omega ^2} + {\omega ^4}) = {a_1}{\omega ^2} + {a_2}{\omega ^4} + {a_3}{\omega ^6} + .. + {a_n}{\omega ^{2n}}\)
Adding the above three equations, we have
\(\begin{array}{l}\log ( - 2\omega ) + \log ( - 2{\omega ^2}) = {a_1}(1 + \omega + {\omega ^2}) + {a_2}(1 + {\omega ^2} + {\omega ^4}) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {a_3}(1 + {\omega ^3} + {\omega ^6}) + ..........\end{array}\)
Now except the terms containing \({a_3},\;{a_6},\;{a_9},...\) all other coefficients will be zero.
\(\log ( - 2\omega \times - 2{\omega ^2}) = 3({a_3} + {a_6} + {a_9} + ...)\)
\( \Rightarrow \log 4 = 3({a_3} + {a_6} + {a_9} + ....)\)
or \({a_3} + {a_6} + {a_9} + .... = \frac{2}{3}\log 2\)

Both the curves will intersect at \(x = \frac{\pi }{4}\) and the enclosed region is ACBDA.
Hence its area is: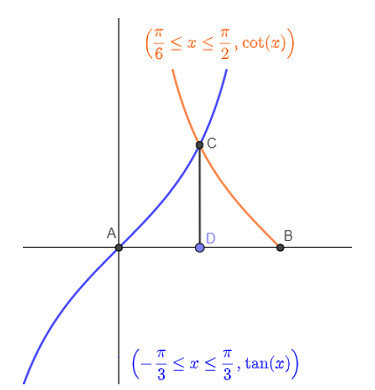

\(\int\limits_0^{\frac{\pi }{4}} {\tan x\,dx} + \int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\cot x\,dx} \) \( = \left[ {\log \sec x} \right]_0^{\pi /4} + \left[ {\log \sin x} \right]_{\pi /4}^{\pi /2}\)
\( = \left[ {\log \sqrt 2 - \log 1} \right] + \left[ {\log 1 - \log \frac{1}{{\sqrt 2 }}} \right] = \log 2\)

Given that \(x + \frac{{100}}{x} > 29 \Rightarrow {x^2} - 29x + 100 > 0\)
Or \((x - 4)(x - 25) > 0\)
\( \Rightarrow x > 25\;{\rm{or}}\;x < 4\)
Thus \(x\)can take a total of 78 values. (1, 2, 3, 26, ……,100)
Required probability = \(\frac{{78}}{{100}} = \frac{{39}}{{50}}\)

We know that \(^{21}{{\rm{C}}_n} = \frac{{21!}}{{n!(21 - n)!}}\)
And \(^{21}{{\rm{C}}_n}\) is maximum when \(n\) is 10 or 11.
So \(n!(21 - n)!\) is minimum when \(n\) = 10, 11.

The first value of \(\theta \) satisfying the equations \(\tan \theta = \frac{1}{{\sqrt 3 }},\;\sin \theta = - \frac{1}{2}\) lies in third quadrant and the value is \(\pi + \frac{\pi }{6} = \frac{{7\pi }}{6}\). The general value of \(\theta \) can be obtained by adding a multiple of \(2\pi \).
General value = \(2n\pi + \frac{{7\pi }}{6}\)

Number of diagonals in a polygon is
\(^n{{\rm{C}}_2} - n\)= 44
\( \Rightarrow \frac{{n(n - 3)}}{2} = 44\) or \(n = 11\)

We know that, \(P(E \cup F) = P(E) + P(F) - P(E \cap F)\)
\( \Rightarrow P(E \cup F) = 0.25 + 0.50 - 0.14 = 0.61\)
Now probability that neither E nor F occurs is \(1 - P(E \cup F) = 1 - 0.61 = 0.39\)

\(\mathop {\lim }\limits_{x \to \infty } {\left( {\frac{{x + 7}}{{x + 2}}} \right)^{x + 5}} = \mathop {\lim }\limits_{x \to \infty } {\left( {{{\left( {1 + \frac{5}{{x + 2}}} \right)}^{x + 2}}} \right)^{\frac{{x + 5}}{{x + 2}}}}\)
\( = \mathop {\lim }\limits_{x \to \infty } {\left( {{e^5}} \right)^{\frac{{x + 5}}{{x + 2}}}} = {e^5}\)

\(A \cup B\) = {1, 2, 3, 4, 5} \(A \cap B\) = {3, 4} \(A\Delta B = (A - B) \cup (B - A)\) = {1, 2, 5}. Hence number of elements in \((A \cup B) \times (A \cap B) \times (A\Delta B)\) is 5×2×3 = 30

Since total frequency is 686, hence F1 + F2 = 686 – sum of all other frequencies
Or F1 + F2 = 106.
Given that median is 42.6, hence the median class is 40 – 50. The formula for median is:
\({\ell _1} + \cfrac{{\,\,\cfrac{n}{2} - C\,\,}}{f}({\ell _2} - {\ell _1})\)
Where \({\ell _1},\;{\ell _2}\) are the lower and upper limit of the class interval, \(n\) is the total frequency, \(C\) is the cumulative frequency of the pre median class and \(f\) is the frequency of the median class.
\( \Rightarrow 42.6 = 40 + \cfrac{{343 - C}}{{180}} \times 10\) or \(C\) = 296
Hence 180 + 34 + F1 = 296 or F1 = 82. So F2 = 24.

We know that when \(f(x)\) is divided by \((x - a)\)the remainder is \(f(a)\). Here to be exactly divisible by \((x - 1)\), the value of polynomial at \(x = 1\)must be 0. Hence \({1^4} - 3({1^3}) + 2p({1^2}) - 6 = 0 \Rightarrow p = 4\)

The median will pass through A and the midpoint of the opposite side i.e \((p,\,\,q)\).
General equation of the line that passes through the intersection point of the lines AC and AB is:
\((px + qy - 1) + \lambda (qx + py - 1) = 0\)
As this line passes through the point \((p,\,\,q)\), hence
\(({p^2} + {q^2} - 1) + \lambda (2pq - 1) = 0 \Rightarrow \lambda = - \frac{{(2pq - 1)}}{{{p^2} + {q^2} - 1}}\)
Putting this value of \(\lambda \), we get the desired equation,
\((px + qy - 1) - \left( {\frac{{2pq - 1}}{{{p^2} + {q^2} - 1}}} \right)(qx + py - 1) = 0\)
Or \((px + qy - 1)({p^2} + {q^2} - 1) - (2pq - 1)(qx + py - 1) = 0\)

The mid points of the diagonals in a parallelogram coincide, hence \(\frac{{P + R}}{2} = \frac{{Q + S}}{2}\) \( \Rightarrow \left( {\frac{{1 + 5}}{2},\,\frac{{2 + 7}}{2}} \right) = \left( {\frac{{4 + a}}{2},\;\frac{{6 + b}}{2}} \right)\) Or \(a = 2,\,\,b = 3\)

Suppose the three vertices are
\(A = 3i + j,{\rm{ }}B = 5i + 2j + k\) and \(C = i - 2j + 3k\)
The side \(AB = 2i + j + k,\;AC = - 2i - 3j + 3k\)
Area of the triangle = \(\frac{1}{2}\left| {AB \times AC} \right| = \frac{1}{2}\left| {6i - 8j - 4k} \right| = \sqrt {29} \)

Suppose \(\left| {\vec a} \right| = k\;{\rm{and}}\;\left| {\vec b} \right| = 2k\)
Also \({k^2} + x(2{k^2})\cos 120 - x{(2k)^2} - k.(2k)\cos 120 = 0\)
\( x = \frac{2}{5}\).

We know that \(\cos 2\theta = \frac{{1 - {{\tan }^2}\theta }}{{1 - {{\tan }^2}\theta }}\)
Given that \(\cos 2\theta = \frac{{1 - {{\tan }^2}\theta }}{{1 - {{\tan }^2}\theta }} = \frac{1}{3} \Rightarrow {\tan ^2}\theta = \frac{1}{2}\)
Putting this value in the equation, we have,
\(32{\left( {\frac{1}{2}} \right)^4} = 2{\cos ^2}\alpha - 3\cos \alpha \)
\( \Rightarrow (2\cos \alpha + 1)(\cos \alpha - 2) = 0\)
Or \(\cos \alpha = - \frac{1}{2} \Rightarrow \alpha = 2n\pi \pm \frac{{2\pi }}{3}\)

Given that the three vectors \(ai + j + k,\,i + bj + k,\;i + j + ck\) are coplanar, hence
\(\left| {\begin{array}{*{20}{c}}a&1&1\\1&b&1\\1&1&c\end{array}} \right| = 0\)
Putting \({C_1} = {C_1} - {C_2},\;{C_2} = {C_2} - {C_3}\),
\(\left| {\begin{array}{*{20}{c}}{a - 1}&0&1\\{1 - b}&{b - 1}&1\\1&{1 - c}&c\end{array}} \right| = 0\)
\( \Rightarrow c(a - 1)(b - 1) - (a - 1)(c - 1) + (1 - b)(1 - c) = 0\)
\( \Rightarrow \frac{c}{{1 - c}} + \frac{1}{{1 - b}} + \frac{1}{{1 - a}} = 0\)
\( \Rightarrow \frac{{c - 1 + 1}}{{1 - c}} + \frac{1}{{1 - b}} + \frac{1}{{1 - a}} = 0\)
Or \(\frac{1}{{1 - c}} + \frac{1}{{1 - b}} + \frac{1}{{1 - a}} = 1\)

Including the 4 geometric means, there are 6 terms in the GP, where the first term is 2 and the last term is 64.
\( \Rightarrow 2({r^5}) = 64\) or \(r = 2\)
The four geometric means are 4, 8, 16, 32.

The equation that is satisfied by both \(\alpha \) and \(\beta \) is \({x^2} = 5x - 3\)or \({x^2} - 5x + 3 = 0\)
Now sum of the roots is:
\(\cfrac{\alpha }{\beta } + \cfrac{\beta }{\alpha } = \cfrac{{{\alpha ^2} + {\beta ^2}}}{{\alpha \beta }} = \cfrac{{{{(\alpha + \beta )}^2} - 2\alpha \beta }}{{\alpha \beta }}\)
\( = \cfrac{{25 - 2 \times 3}}{3} = \cfrac{{19}}{3}\)
Product of the roots is 1, so the equation is: \({x^2} - \frac{{19}}{3}x + 1 = 0\) or \(3{x^2} - 19x + 3 = 0\)

Let us eliminate \(y\) from the first two equations, we have
\(7x + 5z = 4\) ……..(i)
Also eliminate\(y\) from second and third equations,
\(21x + (20 + \lambda )z = 12\)……… (ii)
There will be many solutions if equations (i) and (ii) are identical. Hence \(20 + \lambda = 5 \Rightarrow \lambda = - 5\)

Probability of throwing a triplet is \({\left( {\frac{1}{6}} \right)^3} \times 6 = \frac{1}{{36}}\)
Probability that in all the three throws a triplet is thrown = \(\frac{1}{{36}} \times \frac{1}{{36}} \times \frac{1}{{36}} = {\left( {\frac{1}{{36}}} \right)^3}\)
Probability that a triplet is not thrown more than twice = \(1 - {\left( {\frac{1}{{36}}} \right)^3}\)

Since, each \({A_i}\) has 5 elements, then \(\sum\limits_{i = 1}^{30} {{A_i}} = 30 \times 5 = 150\)
Let set \(S\)consists of \(m\)elements and given that each elements in \(S\) belongs to exactly 10 of \({A_i}'s\), so \(10m = 150 \Rightarrow m = 15\)
Now, since each \({B_i}'s\) has 3 elements and each \(S\) belongs to exactly 9 of \({B_i}'s\)
\( \Rightarrow \sum\limits_{i = 1}^n {{B_i}} = 3 \times n = 3n = 9m = 135\)
Or \(n = 45\)

We know that
\(\sinh x = \cfrac{{{e^x} - {e^{ - x}}}}{2}\) and \(\cosh x = \cfrac{{{e^x} + {e^{ - x}}}}{2}\)c
\(\int {{e^x}(\sinh x + \cosh x)dx} = \int {{e^x}({e^x})dx = \cfrac{{{e^{2x}}}}{2} + C} \)
The choice \({e^x}(\cosh x) = {e^x}\left( {\cfrac{{{e^x} + {e^{ - x}}}}{2}} \right) = \cfrac{{{e^{2x}}}}{2} + C\)
Hence the answer is \({e^x}\cosh x\)

We know that length of the latus rectum = \(\frac{{2{b^2}}}{a}\)and Latus Rectum is perpendicular to the major axis and passes through the focus. Hence coordinates of one of its end are \(\left( {ae,\,\,\frac{{{b^2}}}{a}} \right)\).
If the eccentric angle is \(\theta ,\) then coordinate of the one end of Latus Rectum are \((a\cos \theta ,\;b\sin \theta )\).
Hence \(a\cos \theta = ae,\;b\sin \theta = \frac{{{b^2}}}{a}\)
Or \(\tan \theta = \frac{b}{{ae}}\).
As there are two ends of Latus Rectum, hence \(\theta = {\tan ^{ - 1}}\left( { \pm \frac{b}{{ae}}} \right)\)

\(y = {\sin ^{ - 1}}\left( {\frac{{x + \frac{1}{x}}}{{\sqrt {{x^2} + 3 + \frac{1}{{{x^2}}}} }}} \right) = {\sin ^{ - 1}}\left( {\frac{{x + \frac{1}{x}}}{{\sqrt {{{\left( {x + \frac{1}{x}} \right)}^2} + 1} }}} \right)\)
Let \(x + \frac{1}{x} = \tan \theta \Rightarrow {\sec ^2}\theta \frac{{d\theta }}{{dx}} = 1 - \frac{1}{{{x^2}}}\)
Also \(y = {\sin ^{ - 1}}\left( {\cfrac{{\tan \theta }}{{\sec \theta }}} \right) = \theta \)
So \(\cfrac{{dy}}{{dx}} = \cfrac{{dy}}{{d\theta }} \times \cfrac{{d\theta }}{{dx}} = 1 \times \cfrac{{1 - \frac{1}{{{x^2}}}}}{{{{\sec }^2}\theta }} = \cfrac{{1 - \frac{1}{{{x^2}}}}}{{{{\left( {x + \cfrac{1}{x}} \right)}^2} + 1}}\)
\( = \cfrac{{{x^2} - 1}}{{{x^4} + 3{x^2} + 1}}\)

Given that \(\overrightarrow r \, \times \,\overrightarrow a = \overrightarrow b \times \overrightarrow a \) or \(\overrightarrow r \, \times \,\overrightarrow a - \overrightarrow b \times \overrightarrow a = 0 \Rightarrow (\vec r - \vec b) \times \vec a = 0\)
So the line passes through \(\vec b\)and parallel to \(\vec a\)
\( \Rightarrow \vec r = \vec b + \alpha \vec a\)
Again given that \(\overrightarrow r \, \times \,\overrightarrow b = \overrightarrow a \times \overrightarrow b \)
\( \Rightarrow \vec r = \vec a + \beta \vec b\)
For intersection of both the lines, \(\vec b + \alpha \vec a = \vec a + \beta \vec b\)
By comparing coefficients, \(\alpha = \beta = 1\)
Hence point of intersection is \(\vec a + \vec b = \)3i + j – k

The midpoint of A and B, M is \(\frac{{1 - 1}}{2},\,\frac{{ - 4 + 2}}{2},\,\frac{{3 - 1}}{2} = (0,\, - 1,\,\,1)\)
Hence the vector OM = \( - \widehat j + \mathop k\limits^ \wedge \)

Centre and radius of the first circle are (0, 0) and 2. Centre and radius of the second circle are (3, 4) and 5.
Both the circle touch internally, hence there will be only one common tangent.

We know that \((X \cup Y)' = X' \cap Y'\)
So \(X \cap Y' \cap (X \cup Y)' = X \cap Y' \cap X' \cap Y' = \phi \)

Given that \({e_1} = 2\overrightarrow a + \overrightarrow b \,\,\,\& \,\,{e_2} = \overrightarrow a + 2\overrightarrow b \), hence \(b = \cfrac{{2{e_2} - {e_1}}}{3} = \cfrac{{i + j - 3k}}{3}\)
\(a = \cfrac{{2{e_1} - {e_2}}}{3} = \cfrac{{i + j + 3k}}{3}\)
Now \(a \cdot b = \left| a \right|\,\left| b \right|\cos \theta \) or \(\cfrac{{1 + 1 - 9}}{9} = \cfrac{{\sqrt {11} }}{3} \times \cfrac{{\sqrt {11} }}{3} \times \cos \theta \)
\( \Rightarrow \cos \theta = \cfrac{{ - 7}}{{11}}\).

This is a standard result. The locus will be a circle. This is known as director circle

We can write, \(\cfrac{1}{a} + d = \cfrac{1}{{{H_1}}}\) and \(\cfrac{1}{b} - d = \cfrac{1}{{{H_n}}}\)
Now \(\cfrac{{{H_1} + a}}{{{H_1} - a}} + \cfrac{{{H_n} + b}}{{{H_n} - b}} = \cfrac{{\cfrac{1}{a} + \cfrac{1}{{{H_1}}}}}{{\cfrac{1}{a} - \cfrac{1}{{{H_1}}}}} + \cfrac{{\cfrac{1}{b} + \cfrac{1}{{{H_n}}}}}{{\cfrac{1}{b} - \cfrac{1}{{{H_n}}}}}\)
\( = \cfrac{{\cfrac{1}{a} + \cfrac{1}{a} + d}}{{ - d}} + \cfrac{{\cfrac{1}{b} + \cfrac{1}{b} - d}}{d} = \cfrac{{2\left( {\cfrac{1}{b} - \cfrac{1}{a}} \right) - 2d}}{d} = \cfrac{{2(n + 1)d - 2d}}{d} = 2n\)

tan 9° – tan 27° – tan 63° + tan 81°
= \(\cfrac{{\sin 9^\circ }}{{\cos 9^\circ }} - \cfrac{{\sin 27^\circ }}{{\cos 27^\circ }} - \left[ {\cfrac{{\sin {{63}^ \circ }}}{{\cos {{63}^ \circ }}} - \cfrac{{\sin 81^\circ }}{{\cos 81^\circ }}} \right]\) = A – B
Where A = \(\left( {\cfrac{{\sin {9^ \circ }\cos {{27}^ \circ } - \cos {9^ \circ }\sin {{27}^ \circ }}}{{\cos {9^ \circ }\cos {{27}^ \circ }}}} \right) = \cfrac{{ - \sin {{18}^ \circ }}}{{\cos {9^ \circ }\cos {{27}^ \circ }}}\)\( = \cfrac{{ - 2\sin {9^ \circ }}}{{\cos {{27}^ \circ }}}\)
B = \(\cfrac{{\sin {{63}^ \circ }\cos {{81}^ \circ } - \sin {{81}^ \circ }\cos {{63}^ \circ }}}{{\cos {{63}^ \circ }\cos {{81}^ \circ }}}\)\( = \cfrac{{ - \sin {{18}^ \circ }}}{{\sin {{27}^ \circ }\sin {9^ \circ }}} = \cfrac{{ - 2\cos {9^ \circ }}}{{\sin {{27}^ \circ }}}\)
Hence A – B = \(\cfrac{{2\cos {9^ \circ }}}{{\sin {{27}^ \circ }}} - \cfrac{{2\sin {9^ \circ }}}{{\cos {{27}^ \circ }}}\)\( = \cfrac{{2\left( {\cos {9^ \circ }\cos {{27}^ \circ } - \sin {9^ \circ }\sin {{27}^ \circ }} \right)}}{{\sin {{27}^ \circ }\cos {{27}^ \circ }}}\)
\( = \cfrac{{2\cos {{36}^ \circ }}}{{\left( {\cfrac{{\sin {{54}^ \circ }}}{2}} \right)}} = \cfrac{{4\cos {{36}^ \circ }}}{{\sin {{54}^ \circ }}}\) = 4.

Put \(\tan \theta = x\)
\(y = {\tan ^{ - 1}}\left( {\cfrac{{3\tan \theta - {{\tan }^3}\theta }}{{1 - 3{{\tan }^2}\theta }}} \right) = {\tan ^{ - 1}}(\tan 3\theta ) = 3\theta \)
\(\cfrac{{dy}}{{dx}} = \cfrac{{dy}}{{d\theta }} \times \cfrac{{d\theta }}{{dx}} = 3 \times \cfrac{1}{{{{\sec }^2}\theta }} = \cfrac{3}{{1 + {x^2}}}\)

Let \({3^{{3^{{3^x}}}}} = t\)
\( \Rightarrow {3^{{3^{{3^x}}}}}\log {3.3^{{3^x}}}\log {3.3^x}\log 3dx = dt\)
\( \Rightarrow {3^{{3^{{3^x}}}}}dx = \cfrac{{dt}}{{{{(\log 3)}^3}}}\)
Hence the integration becomes,
\(\int {\cfrac{{dt}}{{{{\left( {\log 3} \right)}^3}}}} = \cfrac{t}{{{{\left( {\log 3} \right)}^3}}} = \cfrac{{{3^{{3^{{3^x}}}}}}}{{{{\left( {\log 3} \right)}^3}}}\)

Let us multiply the two matrices
\(f(\theta )f(\alpha ) = \left[ {\begin{array}{*{20}{c}}{\cos \theta }&{ - \sin \theta }&0\\{\sin \theta }&{\cos \theta }&0\\0&0&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\cos \alpha }&{ - \sin \alpha }&0\\{\sin \alpha }&{\cos \alpha }&0\\0&0&1\end{array}} \right]\)
= \(\left[ {\begin{array}{*{20}{c}}{\cos (\theta + \alpha )}&{ - \sin (\theta + \alpha )}&0\\{\sin (\theta + \alpha )}&{\cos (\theta + \alpha )}&0\\0&0&1\end{array}} \right]\) = \(f(\theta + \alpha )\)

\(\mathop {\lim }\limits_{x \to - 2} \frac{{x + 2}}{{{x^2} + 3x + 2}} = \frac{{(x + 2)}}{{(x + 2)(x + 1)}} = \frac{1}{{(x + 1)}} = - 1\)
Also \(f( - 2) = - 1\)
So the function is continuous at \(x = - 2\)
When \(x \to - 1\), the limit of the function does not exist. Hence the function is not continuous at \(x = - 1\). Correct answer is R – {–1}

Let the three sides are \(a,\,b,\,\,c\), then
\(x = a + b,\,\,y = ab\)
Given that \((a + b + c)(a + b - c) = ab\)
Using \(2s = a + b + c\), we have \(2s(2s - 2c) = ab\)
\( \Rightarrow \left( {\cfrac{{s(s - c)}}{{ab}}} \right) = \cfrac{1}{4}\)
Or \({\cos ^2}\cfrac{C}{2} = \cfrac{1}{4} \Rightarrow \cos \cfrac{C}{2} = \cfrac{1}{2}\)
Thus \(\angle C = 120\) and the triangle is an obtuse angled triangle.