\(\frac{{\sqrt {17} }}{9}\)

We know that distance between the foci is \(2ae\) and sum of the distances from any point on the ellipse from the two foci is \(2a.\)
Hence \(\sqrt {{{(12 - 4)}^2} + {{(5 - 3)}^2}} = 2ae\)
\( \Rightarrow ae = \sqrt {17} \) ………. (1)
Also \(PS + PS' = 2a\), here P is origin as the ellipse passes through origin.
\( \Rightarrow \sqrt {{{12}^2} + {5^2}} + \sqrt {{4^2} + {3^2}} = 2a\)
Or \(a = 9\). Putting the value of \(a\) in the first equation, we get \(e = \frac{{\sqrt {17} }}{9}\).

\(60\)

The number of one-to-one functions from set A to B = \(^n{{\mathop{\rm P}\nolimits} _r}\), where \(r\) and \(n\) are the number of elements in A and B. Hence the answer is \(^5{{\rm{P}}_3} = 5 \times 4 \times 3 = 60\)

\({4!^{1/4}}\)

Given that \(x \to 0\), hence \({1^x} \approx {2^x} \approx {3^x} \approx {4^x} \approx 1\)
Since all the numbers are tending to the same value, we can take their Geometric Mean in place of Arithmetic Mean.
\(\left( {\frac{{{1^x} + {2^x} + {3^x} + {4^x}}}{4}} \right) = {\left( {{1^x}{2^x}{3^x}{4^x}} \right)^{1/4}}\)
And the value of the limit = \({\left[ {{{\left( {{1^x}{2^x}{3^x}{4^x}} \right)}^{1/4}}} \right]^{1/x}}\)
\( = {24^{1/4}} = {(4!)^{1/4}}\)

\(1\)

Volume of the parallelepiped is given by
\(\left| {\begin{array}{left{20}{c}}m&1&1\\1&{ - 1}&1\\1&2&{ - 1}\end{array}} \right| = 4\)
\( \Rightarrow m( - 1) - 1( - 2) + (3) = 4\)
\( \Rightarrow m = 5 - 4 = 1\)

\(2\)

For coplanar vectors, the scalar triple product is zero. Hence
\(\left| {\begin{array}{left{20}{c}}{{\lambda ^2}}&1&1\\1&{{\lambda ^2}}&1\\1&1&{{\lambda ^2}}\end{array}} \right| = 0\)
Apply \({C_1} = {C_1} + {C_2} + {C_3}\)
\(({\lambda ^2} + 2)\left| {\begin{array}{left{20}{c}}1&1&1\\1&{{\lambda ^2}}&1\\1&1&{{\lambda ^2}}\end{array}} \right| = 0\)
Apply \({R_1} = {R_1} - {R_2}\)
\(({\lambda ^2} + 2)\left| {\begin{array}{left{20}{c}}0&{1 - {\lambda ^2}}&0\\1&{{\lambda ^2}}&1\\1&1&{{\lambda ^2}}\end{array}} \right| = 0\)
\( \Rightarrow ({\lambda ^2} + 2)(1 - {\lambda ^2})(1 - {\lambda ^2}) = 0\)
Hence \(\lambda = \pm 1\). There are two possible values.

\(9 \times {\,^9}{{\rm{C}}_5}\)

Given that exactly 5 bottles are going to the corresponding numbered boxes, and the remaining 4 are placed in the wrong boxed. This can be done in \(^9{{\rm{C}}_5} \times {D_4}\), where \({D_4}\)is the derangements of 4 objects.
Required answer = \(^9{{\rm{C}}_5} \times 9\)

– 4 and 4

As the perpendicular bisector is equidistant from the points P and Q. Hence the point (0, – 4) has same distance from the points P and Q.
\( \Rightarrow \sqrt {{k^2} + {{(3 + 4)}^2}} = \sqrt {{1^2} + {{(4 + 4)}^2}} \)
\( \Rightarrow k = \pm 4\)

None of these

Given that \(x\) and \(y\) are natural numbers, there are many solutions to the equation \({x^2} - {2^y} = 0\). Some of them are (2, 2), (4, 4), (8, 6), (16, 8) etc. This question was wrong.

\(16\)

\(x = 1 + \sqrt[6]{2} + \sqrt[6]{4} + \sqrt[6]{8} + \sqrt[6]{{16}} + \sqrt[6]{{32}}\)
Let us assume that \(\sqrt[6]{2} = a\), then
\(x = 1 + a + {a^2} + {a^3} + .... + {a^5} = \frac{{{a^6} - 1}}{{a - 1}}\)
\( \Rightarrow x = \frac{{2 - 1}}{{\sqrt[6]{2} - 1}} = \frac{1}{{\sqrt[6]{2} - 1}}\)
Hence \(1 + \frac{1}{x} = 1 + \sqrt[6]{2} - 1 = \sqrt[6]{2}\)
\( \Rightarrow {\left( {1 + \frac{1}{x}} \right)^{24}} = {\left( {\sqrt[6]{2}} \right)^{24}} = 16\)

\(4\)

Let us assume that \(|\sin x| = a\), then
\({5^{\,\frac{1}{{1 - a}}}} = 25\)
\( \Rightarrow \frac{1}{{1 - a}} = 2\) or \(a = \frac{1}{2}\)
So \(\sin x = \pm \frac{1}{2}\), so there are 4 solutions in the interval \(( - \pi ,\,\,\pi )\)

\(\lambda = 2,{\mkern 1mu} \,\mu = 5\)

Subtract equation (1) from (2), we get \(z = 1\)
Subtract equation (2) from (3), we get \((\lambda - 3)z = \mu - 6\)
Putting value of \(z\), we get \(\lambda - 3 = \mu - 6\)
There are many values of \(\lambda ,\;\mu \)for which the equations will have many solutions. Choice (3) is the correct answer.

\(\int_0^3 {{e^{{x^2}}}} dx = \int_0^5 {{e^{{x^2}}}} dx + \int_5^3 {{e^{{x^2}}}} dx\)

Only choice (2) is correct.

\(60J\)

Work done = \(\left| F \right|\left| D \right|\cos \theta = 40 \times 3 \times \frac{1}{2} = 60\)
Choice (4)

\(\frac{4}{9}\)

Requires probability
P (couple is there) + P (couple is not there)
= \(\frac{{1 \times {\,^7}{{\rm{C}}_3}}}{{^9{{\rm{C}}_5}}} + \frac{{^7{{\rm{C}}_5}}}{{^9{{\rm{C}}_5}}} = \frac{{56}}{{126}} = \frac{4}{9}\)
Choice (4)

\(48\)

Assume \(4x = \theta \), then the equation becomes \(\sin \theta = \frac{1}{2}\) and \( - 36\pi < \theta < 12\pi \)
We can shift the interval to \(0 < \theta < 48\pi \)
In the interval \((0,\;2\pi )\), \(\sin \theta = \frac{1}{2}\) has two solutions, hence in the interval \(0 < \theta < 48\pi \), there will be 48 solutions. Hence the cardinality of the set \(C\)= 48.

\(2\)

The axis of hyperbola lies along \(y\) axis and major axis of the ellipse also lies on \(y\) axis. Centre of the ellipse is (0, 4) and length of its major axis is 8. Thus, it passes through origin.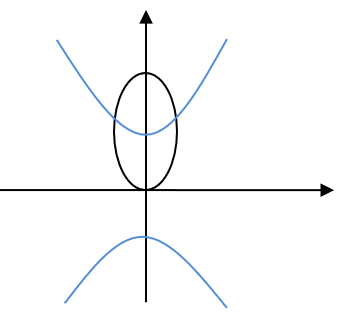

Hence there will be only two intersection points.

\(\frac{{(c - d)(3e - 2)}}{{{c^2} - {d^2}}}\)

Put \(x = \frac{1}{x}\) in the given equation,
\(cf(x) + df\left( {\frac{1}{x}} \right) = \left| {\log |x|} \right| + 3\) ….. (1)
\(cf\left( {\frac{1}{x}} \right) + df(x) = \left| {\log \left| {\frac{1}{x}} \right|} \right| + 3{\rm{ }}\)
We know that \(\log \left( {\frac{1}{x}} \right) = - \log x\)
Hence \(cf\left( {\frac{1}{x}} \right) + df(x) = \left| {\log \left| x \right|} \right| + 3{\rm{ }}\)….(2)
Eliminating \(f\left( {\frac{1}{x}} \right)\)from the two equations, we get
\(f(x) = \frac{{(c - d)}}{{{c^2} - {d^2}}}(\log |x| + 3)\)
\( \Rightarrow \int\limits_1^e {f(x)dx = \frac{{c - d}}{{{c^2} - {d^2}}}\int\limits_1^e {(\log x + 3)\,dx} } \)
Integrating and putting the values of the limits,
\(\frac{{c - d}}{{{c^2} - {d^2}}}\left[ {x\log x - x + 3x} \right]_1^e\)
\( = \frac{{c - d}}{{{c^2} - {d^2}}}\left[ {3e - 2} \right]\)

\(0.432\)

The required probability
= \(^3{{\rm{C}}_2}{(0.6)^2}{(0.4)^1} = 0.432\)

\( - 1\)

Using the formula \(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 - \tan x\tan y}}\)
\(\frac{{\tan \frac{\pi }{4} + \tan \theta }}{{1 - \tan \frac{\pi }{4}\tan \theta }} \times \frac{{\tan \frac{{3\pi }}{4} + \tan \theta }}{{1 - \tan \frac{{3\pi }}{4}\tan \theta }}\)
= \(\frac{{1 + \tan \theta }}{{1 - \tan \theta }} \times \frac{{ - 1 + \tan \theta }}{{1 + \tan \theta }} = - 1\)
Choice (4)

\(2\pi \)

The period of \(\sin x\) and \(\cos x\) is \(2\pi \)
Hence \(x - y = 2\pi \)

\(\left| {A({\rm{adj}}(A))} \right| \ne 1\)

We know that \(\left| {A({\rm{adj}}(A))} \right| = {\left| A \right|^{n - 1}}\)
This value should be non-zero, this can be 1.
Choice (4)

\( - 6{\rm{ and }} - 35\)

We know that angle between the lines is given by
\(\tan \theta = \frac{{2\sqrt {{h^2} - ab} }}{{a + b}}\)
\( \Rightarrow 1 = \frac{{2\sqrt {\frac{1}{4} - 6\lambda } }}{{6 + \lambda }}\)
Solving this equation, we get \(\lambda = - 35\)

\(\frac{1}{2}\)

Required probability
= \(0.40 (1 - 0.50) + (1 - 0.40) 0.50 = 0.5\)

\(c > 2(a - b)\)

Equation of normal of the parabola \({y^2} = 4a(x + c)\)is
\(y = m(x + c) - 2am - a{m^3}\)
\( \Rightarrow y = mx + mc - 2am - a{m^3}\)
Similarly, equation of normal for the parabola \({y^2} = 4bx\) is:
\(y = mx - 2bm - b{m^3}\)
As the normal is common, hence
\(mc - 2am - a{m^3} = - 2bm - b{m^3}\)
\((a - b){m^3} = m(c + 2b - 2a)\)
\( \Rightarrow {m^2} = \frac{{c + 2b - 2a}}{{a - b}} = \frac{c}{{a - b}} - 2\)
As \({m^2} > 0\), hence \(\frac{c}{{a - b}} - 2 > 0 \Rightarrow c > 2(a - b)\)

\(\frac{1}{{\sqrt 2 }}( - \hat i + 7\hat j)\)

His movement can be represented as
\(3\left( {\frac{{i + j}}{{\sqrt 2 }}} \right) + 4\left( {\frac{{ - i + j}}{{\sqrt 2 }}} \right)\)
\(\frac{1}{{\sqrt 2 }}\left( { - i + 7j} \right)\)

355

The difference between all the remainder from the divisors is 5, hence the answer should be
\(\text{LCM}(9, 10, 15, 20)k - 5\)
\( = 180k - 5\)
There is only one such number 355.

\(1 - {2^{ - n}}\)

We know that \(\frac{{^n{P_r}}}{{r!}} = {\,^n}{C_r}\)
Hence the given sum is
\(\frac{1}{{{2^n}}}\sum\limits_{r = 1}^n {^n{C_r}} = \frac{1}{{{2^n}}}\left( {^n{C_1}{ + ^n}{C_2} + ...{ + ^n}{C_n}} \right)\)
\( = \frac{1}{{{2^n}}}({2^n} - 1) = 1 - \frac{1}{{{2^n}}}\) Choice (2)

\(P(A) + P(B) - 2P(A \cap B)\)

The even \(P\left( {(A \cap {B^C}) \cup ({A^C} \cap B)} \right)\) mean that either only event A occurs, or event B occurs. This probability is equal to \(P(A \cup B) - P(A \cap B)\)

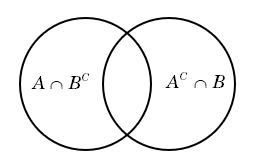
\( = P(A) + P(B) - 2P(A \cap B)\)

1

The integers solutions of the equation \({x^2} + 2{y^2} = 3\) are \({x^2} = 1\) and \({y^2} = 1\), the possible values of \((x,y)\) are (1, 1), (1, – 1), (– 1, 1), and (–1, – 1). Only in one case \(x > y\), hence number of elements in \(X \cap Y\)will be only one.

2

Put \(x = 0\) in the function to get the value of \(f(1).\)
\(f(1) = 0 + 2 = 2\)

At least 2

The median of the combined data will be at least 2.

\(f'(x)\) is not continuous at \(x = 0\)

We know that for any value of \(x,\,\)\(\sin x\) is finite and its values remains between –1 and 1.
\(f'({0^ + }) = \frac{{{h^2}\sin \left( {\frac{1}{h}} \right) - 0}}{h} = h\sin \left( {\frac{1}{h}} \right) = 0\)
\(f'({0^ - }) = \frac{{{h^2}\sin \left( { - \frac{1}{h}} \right) - 0}}{{ - h}} = h\sin \left( {\frac{1}{h}} \right) = 0\)
Hence function is differentiable at \(x = 0\)
\(f'(x) = 2x\sin \left( {\frac{1}{x}} \right) + {x^2}\cos \left( {\frac{1}{x}} \right)\left( { - \frac{1}{{{x^2}}}} \right)\)
\( \Rightarrow f'(x) = 2x\sin \left( {\frac{1}{x}} \right) - \cos \left( {\frac{1}{x}} \right)\)
When \(x \to 0\), \(\cos \left( {\frac{1}{x}} \right)\) does not give a definite value, hence \(f'(x)\) is not continuous at \(x = 0\)

\(\frac{1}{2}\)

We know that the probability of getting head in an even number of times is same as that of getting an odd number of times.
Hence the probability = \(\frac{1}{2}\)

\(f\) has a point of inflection at \(x = 6\)

\(f(x) = {x^{2/3}}{(6 - x)^{1/3}}\)
\(f'(x) = \frac{2}{3}{x^{ - \frac{1}{3}}}{(6 - x)^{\frac{1}{3}}} - \frac{1}{3}{(6 - x)^{ - \frac{2}{3}}}{x^{\frac{2}{3}}}\)
\( = {(6 - x)^{ - \frac{2}{3}}}{x^{ - \frac{1}{3}}}(4 - x)\)
We see that the value of \(f'(x) > 0\)in the interval (0, 4), also the value of \(f'(x) < 0\) when \(x > 6\).
Also \(f''(x) = 0\)at \(x = 6\), hence\(f(x)\) has a point of inflection at \(x = 6\)

\(0\)

\(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - {e^{ - x}} - 2x}}{{1 - \cos x}} = \frac{{{e^x} + {e^{ - x}} - 2}}{{\sin x}}\)
\( = \mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - {e^x}}}{{\cos x}} = 0\)

\(f(x)\) has a local maximum at \(x = 2\), which is not the global maximum

To find maxima or minima, let us differentiate the function.
\(f'(x) = - 3{x^2} + 6x = 0\)
\( \Rightarrow x = 0,\;2\)
At \(x = 2,\) the function is maximum, and its value is 5. Hence it is bigger than the value of \(\cos x\) and \({e^{ - x}}\). But the graph of cubic function can achieve even bigger values at negative values of \(x\), for example \(f( - 2) = 21\), hence at \(x = 2\), the function achieves only the local maxima.

\(2apq\)

Let the two numbers are \(x,\;y\), then
\(x,\;a,\;y\) are in AP and
\(x,\;p,\;q,\;y\) are in GP.
Hence \(2a = x + y\) and \(\frac{p}{x} = \frac{q}{p} = \frac{y}{q}\)
\( \Rightarrow x = \frac{{{p^2}}}{q},\;y = \frac{{{q^2}}}{p}\;\)
Putting these values, we get \(2a = \frac{{{p^2}}}{q} + \frac{{{q^2}}}{p}\)
Or \({p^3} + {q^3} = 2apq\)

An ellipse

We see that \(h = 5,\;a = 3,\;b = 11,\;g = 7,\;f = 6,\;c = 5\)
\(abc + 2fgh - a{f^2} - b{g^2} - c{h^2} \ne 0\)
And \({h^2} < ab\), hence it is an ellipse.

On the opposite side of the line \(2x + 3y = - 6\)

Put the points in the given line and check the signs. If the signs are same, then the points are on the same side of the line otherwise they are on different sides of the lines.
The first line is \(2x + 3y - 6 = 0\) and the second line is \(2x + 3y + 6 = 0\)
At point \(\left( {1,\;\frac{1}{2}} \right)\), the first line is negative, but the second line is positive.
At the point \(\left( {3,\; - \frac{1}{2}} \right)\), the first line is negative, but the second line is positive.
Only choice (4) is wrong. The first three choices are correct.
both the lines are of opposite signs. Hence this point lies between the lines. Similarly, the point \(\left( {3,\; - \frac{1}{2}} \right)\)also lies between the lines.

\(3.18198 \times {10^3}J\)

The work done is \(\overline F \cdot \overline d = \,\left| F \right|\left| d \right|\cos \theta \)
\(180 \times 25 \times \cos 45 = 3181.98\;J\)

Sink field

The divergence of the vector \(\bar A\)is given bu
\({\rm{div}}(\bar A) = \frac{{\partial {A_x}}}{{\partial x}} + \frac{{\partial {A_y}}}{{\partial y}} + \frac{{\partial {A_z}}}{{\partial z}}\)
Here \({A_x} = 2x + 1,\;{A_y} = ({x^2} - 6y),\;{A_z} = (x{y^2} + 3z)\)
Hence \({\rm{div}}(\bar A) = 2 - 6 + 3 = - 1\)
If \({\rm{div}}(\bar A) > 0\), the field is a source field.
If \({\rm{div}}(\bar A) < 0\), the field is a sink field.
If \({\rm{div}}(\bar A) = 0\), the field is a solenoidal field.
Since \({\rm{div}}(\bar A) = - 1\), the vector field is a sink field.

\(\frac{1}{2}\)

We know that \({x^2} + {y^2} = 4\) is a circle and its one fourth part lies in the first quadrant. In the point \(P = (r,s)\), \(r\) and \(s\) are \(x\) and \(y\) coordinates, and we need to find the probability that \(x > y\).
The shaded part is the favourable area and the area of the circle in the first quadrant is the sample space.

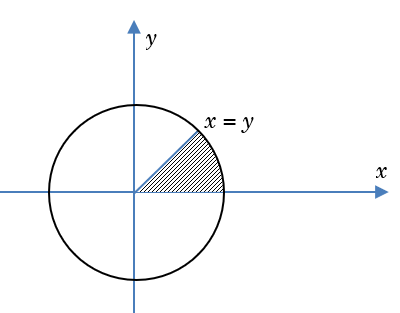
Hence the required probability = \(\frac{1}{2}\)

\(26\)

Total number of intersection points (in normal case when no two lines are parallel or no three pass through the same point) \(^{10}{C_2}\)
But the five lines \({L_2},{L_4},{L_6},{L_8},{L_{10}}\)are parallel, hence these lines do not intersect.
Also the five lines \({L_1},{L_3},{L_5},{L_7},{L_9}\)intersect at the same point, hence these lines create only one intersecting point.
Number of intersecting points is:
\(^{10}{C_2} - {\,^5}{C_2} - {\,^5}{C_2} + 1 = 26\)

\(a < 0\)

Let any point on the curve \(xy = 1\)is \(\left( {t,\;\frac{1}{t}} \right)\), to calculate the slope of tangent at this point, let us differentiate the function,
\(xy' + y = 0 \Rightarrow y' = - \frac{y}{x}\)
Slope of the tangent = \( - \frac{{1/t}}{t} = - \frac{1}{{{t^2}}}\)
Slope of the normal = \({t^2}\)
As \({t^2} > 0\), slope of the normal should be positive.
\( \Rightarrow - \frac{{{a^2}}}{a} > 0\) or \(a < 0\)

\(14\)

Let the number of students passed in mathematics, Physics and Chemistry are denoted by \(M,\;P\) and \(C,\) then,
\(50 = M + P + C - (M \cap P + P \cap C + M \cap C)\)
\( + M \cap P \cap C\)
\( \Rightarrow M \cap P \cap C\)
\( = 50 + 19 + 29 + 20-37-24-43 = 14\)

None of the above

Let us check the limit of the function at \(x = 0\),
\(\mathop {\lim }\limits_{x \to 0} \frac{x}{{{e^{\pi x}} - 1}} = \frac{1}{{\pi {e^{\pi x}}}} = \frac{1}{\pi }\)
Hence the function us continuous at \(x = 0\).
Let us check derivative of the function at \(x = 0\)
\(f'({0^ + }) = \mathop {\lim \,}\limits_{h \to 0} \frac{{f(0 + h) - f(0)}}{h}\)
\( = \mathop {\lim }\limits_{h \to 0} \,\,\frac{{\frac{h}{{{e^{\pi h}} - 1}} - \frac{1}{\pi }}}{h}\)
\( = \mathop {\lim }\limits_{h \to 0} \frac{{h\pi - ({e^{h\pi }} - 1)}}{{h\pi ({e^{h\pi }} - 1)}} = \frac{{h\pi - \left( {h\pi + \frac{{{h^2}{\pi ^2}}}{{2!}} + } \right)}}{{h\pi \left( {h\pi + \frac{{{h^2}{\pi ^2}}}{{2!}} + } \right)}}\)
\( = \frac{{ - \frac{{{h^2}{\pi ^2}}}{{2!}} + ....}}{{{h^2}{\pi ^2} + \frac{{{h^3}{\pi ^3}}}{{2!}} + ...}} = - \frac{1}{2}\)
Similarly, it can be shown that
\(f'({0^ - }) = \frac{1}{2}\)
Correct answer is (4).

\( - 1\)

Since \({\pi ^2} \approx 9.8\), hence \({\pi ^2} = 9\) and \([ - {\pi ^2} = - 10\)
The given question is \(\cos 9x + \cos ( - 10x)\)
\(\cos 9x + \cos (10x)\)
\(f\left( {\frac{\pi }{2}} \right) = \cos \frac{{9\pi }}{2} + \cos \frac{{10\pi }}{2} = - 1\)

\(\frac{4}{{1155}}\)

All the three numbers should be multiple of 6, as there are 16 multiples of 6 in the first 100 natural numbers, hence the required probability
\( = \frac{{^{16}{{\rm{C}}_3}}}{{^{100}{{\rm{C}}_3}}} = \frac{{16 \times 15 \times 14}}{{100 \times 99 \times 98}} = \frac{4}{{1155}}\)

\(1,4\)

We know that 3(median) – Mode = 2(Mean)
\( \Rightarrow 3 \times {3^x} - {9^x} = 2 \times 1\)
\( \Rightarrow {y^2} - 3y + 2 = 0\), where \(y = {3^x}\)
\( \Rightarrow y = 1,\;2\)
Hence possible value of mode = 1, 4

\({e^{ - 1}}\)

\({n^{{\rm{th}}}}\)term is given by \(\frac{{2n}}{{(2n + 1)!}} = \frac{{2n + 1 - 1}}{{(2n + 1)!}} = \frac{1}{{2n!}} - \frac{1}{{(2n + 1)!}}\)
\( = \left( {\frac{{e + {e^{ - 1}}}}{2} - 1} \right) - \left( {\frac{{e - {e^{ - 1}}}}{2} - 1} \right)\)\( = {e^{ - 1}}\)